题目内容
7．
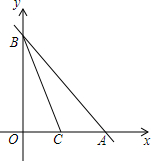如图，在平面直角坐标系中，直线y=-x+4与坐标轴分别交A，B两点，点C（2，0），连接BC，点P为线段AB上一动点，连接OP，OP交BC于点D（1）直接写出点的坐标A（4，0），B（0，4）；
（2）当S△OCD=S△BPD时，求此时P点坐标．
分析 （1）将x=0，y=0代入解析式解答即可；
（2）根据等式的性质得出△BOP与△BOC的面积相等，进而得出点P的坐标即可．
解答 解：（1）把x=0代入y=-x+4=4，
把y=0代入y=-x+4，解得：x=4，
所以点A的坐标为（4，0），点B的坐标为（0，4），
故答案为：（4，0）；（0，4）；
（2）如图，
∵S△OCD=S△BPD，
∴S△BOP=S△BOC，
因为△BOP与△BOC的底边都是OB，所以点P的横坐标与点C的横坐标相等，即x=2，
把x=2代入直线y=-x+4=2，
所以点P的坐标为（2，2）．
点评 此题考查一次函数的问题，关键是根据一次函数与坐标轴的交点进行解答．
练习册系列答案
阅读快车系列答案
相关题目
17．某项工程，甲单独做20小时完成，乙单独做21小时完成，现由甲单独做5小时，剩下的甲、乙合做，还需几小时完成？若设剩下的部分要x小时完成，下列方程正确的是（ ）
| A． | $\frac{5}{20}$-$\frac{x}{20}$-$\frac{x}{21}$=1 | B． | $\frac{5}{20}$+$\frac{x}{20}$-$\frac{x}{21}$=1 | C． | $\frac{5}{20}$+$\frac{x}{20}$+$\frac{x}{21}$=1 | D． | $\frac{5}{20}$-$\frac{x}{20}$+$\frac{x}{21}$=1 |
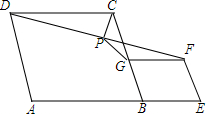如图，在菱形ABCD和菱形BEFG中，点A、B、E在同一直线上，P是线段DF的中点，连接PG、PC．若∠ABC=60°，AB=3，BE=1，则PG的长度=$\sqrt{3}$．
已知：如图，在等边三角形ABC中，D、E、F分别为各边的中点，求证：四边形DEFB是平行四边形．