题目内容
20. 如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{3\sqrt{5}}{2}$ | C. | 2$\sqrt{3}$ | D. | $\frac{\sqrt{41}}{2}$ |
分析 根据等腰三角形的性质可得点D是AB的中点,然后根据三角形中位线定理可得DP=$\frac{1}{2}$BG,然后利用两点之间线段最短就可解决问题.
解答 解:连接BG,如图.
∵CA=CB,CD⊥AB,AB=6,
∴AD=BD=$\frac{1}{2}$AB=3.
又∵CD=4,
∴BC=5.
∵E是高线CD的中点,
∴CE=$\frac{1}{2}$CD=2,
∴CG=CE=2.
根据两点之间线段最短可得:BG≤CG+CB=2+5=7.
当B、C、G三点共线时,BG取最大值为7.
∵P是AG中点,D是AB的中点,
∴PD=$\frac{1}{2}$BG,
∴DP最大值为$\frac{7}{2}$.
故选A.
点评 本题主要考查了圆的综合题,涉及了等腰三角形的性质、三角形中位线定理、勾股定理、两点之间线段最短等知识,利用三角形中位线定理将DP转化为BG是解决本题的关键.

练习册系列答案
相关题目
 如图,在平行平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,求平行四边形ABCD的周长.
如图,在平行平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,求平行四边形ABCD的周长.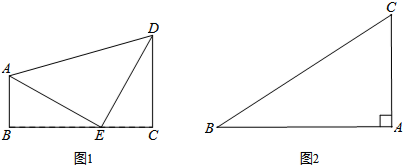
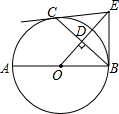 如图,已知AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连结BE.
如图,已知AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连结BE.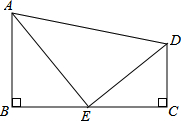 如图,∠B=∠C=90°,AE平分∠BAD,DE平分∠ADC,若S△CDE=$\frac{2}{3}$S△ABE,则S△DEC:S△ADE=2:5.
如图,∠B=∠C=90°,AE平分∠BAD,DE平分∠ADC,若S△CDE=$\frac{2}{3}$S△ABE,则S△DEC:S△ADE=2:5. 如图,△ABC中,∠ABC、∠ACB的平分线相交于点I.若∠ACB=70°,∠ABC=50°,则∠BIC=120°.
如图,△ABC中,∠ABC、∠ACB的平分线相交于点I.若∠ACB=70°,∠ABC=50°,则∠BIC=120°.