题目内容
5.用[x]表示不超过x的最大整数,如[-3.4]=-4,[3]=3,[π]=3,…(1)求证:[x]+[x+$\frac{1}{2}$]=[2x];
(2)解方程:[$\frac{6x+5}{8}$]=$\frac{15x-7}{5}$.
分析 (1)分别从当0≤x-[x]<$\frac{1}{2}$时与当$\frac{1}{2}$≤x-[x]<1时,去分析求解即可求得答案;
(2)由题意变形的:0≤$\frac{6x+5}{8}$-$\frac{15x-7}{5}$<1①;$\frac{15x-7}{5}$=A(A为整数)②;然后分别将①②,即可得0.9≤$\frac{5A+7}{15}$<$\frac{121}{90}$,继而求得A的值,则可求得x的值.
解答 (1)证明:当0≤x-[x]<$\frac{1}{2}$时,[x+$\frac{1}{2}$]=[x],[2x]=2[x],
∴[x]+[x+$\frac{1}{2}$]=[2x];
当$\frac{1}{2}$≤x-[x]<1时,[x+$\frac{1}{2}$]=[x]+1,[2x]=2[x]+1,
∴[x]+[x+$\frac{1}{2}$]=[2x];
综上,[x]+[x+$\frac{1}{2}$]=[2x];
(2)解:由题意变形的:0≤$\frac{6x+5}{8}$-$\frac{15x-7}{5}$<1①;$\frac{15x-7}{5}$=A(A为整数)②;
分别由①变形进行不等式计算得:0.9≤x<$\frac{121}{90}$③;
由②变形进行变形得:x=$\frac{5A+7}{15}$④;
把③中x的代换④中,0.9≤$\frac{5A+7}{15}$<$\frac{121}{90}$,
化简变形的:1.3≤A<$\frac{79}{30}$,
∴A=2,
∴x=$\frac{17}{15}$.
点评 此题考查了取整函数的性质.注意利用[x]≤x<[x]+1可得到关于x的不等式,并求出x的可能值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
 如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{3\sqrt{5}}{2}$ | C. | 2$\sqrt{3}$ | D. | $\frac{\sqrt{41}}{2}$ |
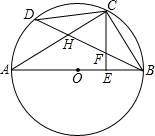 如图,AB是⊙O的直径,C是$\widehat{BD}$的中点,CE⊥AB于E,BD交CE于点F,BD交CA于点H.
如图,AB是⊙O的直径,C是$\widehat{BD}$的中点,CE⊥AB于E,BD交CE于点F,BD交CA于点H.
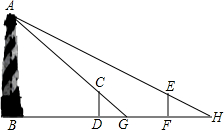 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2米到点G处,在G处测得建筑物项端A标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,则建筑物的高是54米.
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2米到点G处,在G处测得建筑物项端A标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,则建筑物的高是54米.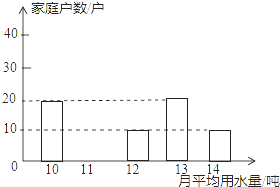 自来水公司对某社区600户居民家庭的用水情况做了一次调查.调查小组随机抽查了其中的100户家庭一年的月平均用电量(单位:吨),并将调查结果制成了如图所示的条形统计图.
自来水公司对某社区600户居民家庭的用水情况做了一次调查.调查小组随机抽查了其中的100户家庭一年的月平均用电量(单位:吨),并将调查结果制成了如图所示的条形统计图.