题目内容
12.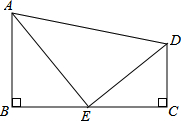 如图,∠B=∠C=90°,AE平分∠BAD,DE平分∠ADC,若S△CDE=$\frac{2}{3}$S△ABE,则S△DEC:S△ADE=2:5.
如图,∠B=∠C=90°,AE平分∠BAD,DE平分∠ADC,若S△CDE=$\frac{2}{3}$S△ABE,则S△DEC:S△ADE=2:5.
分析 过点E作EF⊥AD于F,根据角平分线上的点到角的两边距离相等可得BE=EF,然后利用“HL”证明Rt△ABE和Rt△AFE全等,根据全等三角形的面积相等可得S△ABE=S△AFE,同理可得S△DEC=S△DEF,设S△ABE=3k,表示出S△CDE,然后求解即可.
解答 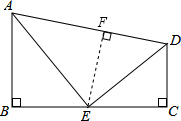 解:如图,过点E作EF⊥AD于F,
解:如图,过点E作EF⊥AD于F,
∵∠B=90°,AE平分∠BAD,
∴BE=EF,
在Rt△ABE和Rt△AFE中,$\left\{\begin{array}{l}{AE=AE}\\{BE=EF}\end{array}\right.$,
∴Rt△ABE≌Rt△AFE(HL),
∴S△ABE=S△AFE,
同理可得S△DEC=S△DEF,
设S△ABE=3k,
∵S△CDE=$\frac{2}{3}$S△ABE,
∴S△CDE=2k,
∴S△DEC:S△ADE=2k:(3k+2k)=2:5.
故答案为:2:5.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
7.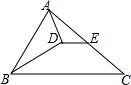 如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
 如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )| A. | ∠BAD=∠C+∠DAE | B. | DE∥BC | C. | DE=$\frac{1}{2}(BC-AB)$ | D. | BD=EC |
20. 如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
 如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{3\sqrt{5}}{2}$ | C. | 2$\sqrt{3}$ | D. | $\frac{\sqrt{41}}{2}$ |
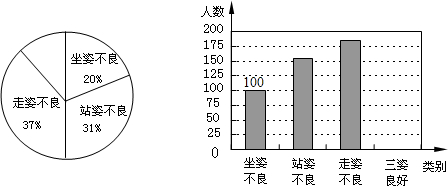
4.金华联超市对销量较大的A、B、C三种品牌的洗衣粉进行了问卷调查,发放问卷309份(问卷由单选题和多选题组成).对收回的250份问卷进行整理,部分数据如下:
(一)最近一次购买各品牌洗衣粉(单选题)的用户情况(如图1)
(二)用户对各品牌洗衣粉满意(多选题)的情况(如表)
根据以上信息解决下列问题:
(1)在图2中,将最近一次购买各品牌洗衣粉的用户情况绘制成条形统计图;
(2)上述调查中哪种品牌洗衣粉的销售量最大?它的主要竞争优势是什么?
(3)广告对用户选择品牌有影响吗?请简要说明你判断的理由.
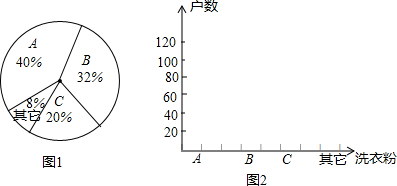
(一)最近一次购买各品牌洗衣粉(单选题)的用户情况(如图1)
(二)用户对各品牌洗衣粉满意(多选题)的情况(如表)
| 内 容 | 质 量 | 广 告 | 价 格 | ||||||
| 品 牌 | A | B | C | A | B | C | A | B | C |
| 满意的户数 | 198 | 116 | 122 | 144 | 172 | 107 | 98 | 85 | 111 |
(1)在图2中,将最近一次购买各品牌洗衣粉的用户情况绘制成条形统计图;
(2)上述调查中哪种品牌洗衣粉的销售量最大?它的主要竞争优势是什么?
(3)广告对用户选择品牌有影响吗?请简要说明你判断的理由.

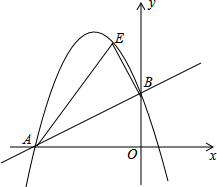 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=-x2+bx+c,点E为第二象限内抛物线上一动点,连接AE,BE.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=-x2+bx+c,点E为第二象限内抛物线上一动点,连接AE,BE. 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标为($\frac{3}{2}$,3).
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标为($\frac{3}{2}$,3).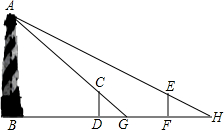 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2米到点G处,在G处测得建筑物项端A标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,则建筑物的高是54米.
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2米到点G处,在G处测得建筑物项端A标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,则建筑物的高是54米.