题目内容
20. 如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是①③④.(填写序号)
如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是①③④.(填写序号)
分析 ∠1=∠2,∠BAC=∠EAD,AC=AD,根据三角形全等的判定方法,可加一角或已知角的另一边.
解答 解:已知∠1=∠2,AC=AD,由∠1=∠2可知∠BAC=∠EAD,
加①AB=AE,就可以用SAS判定△ABC≌△AED;
加③∠C=∠D,就可以用ASA判定△ABC≌△AED;
加④∠B=∠E,就可以用AAS判定△ABC≌△AED;
加②BC=ED只是具备SSA,不能判定三角形全等.
其中能使△ABC≌△AED的条件有:①③④;
故答案为①③④.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.做题时要根据已知条件在图形上的位置,结合判定方法,进行添加.

练习册系列答案
相关题目
11.下列等式中是一元一次方程的是( )
| A. | S=$\frac{1}{2}$ab | B. | x-y=0 | C. | x=0 | D. | $\frac{1}{2x+3}$=1 |
5.定义:我们把关于x的一元二次方程ax2+bx+c=0与cx2+bx+a=0(ac≠0,a≠c)称为一元二次方程的一对“和谐方程”.
(1)正确填写表格中的空白.
(2)根据表1,猜想原方程的两根与“和谐方程”的两根之间关系,并证明.
(3)已知关于x的方程2016x2+bx-1=0的两根是x1=-1,x2=$\frac{1}{2016}$.请利用(2)中的结论,解关于x的方程:(x-1)2-bx+b=2016.
(1)正确填写表格中的空白.
| 原方程 | 原方程的根 | ”和谐方程“ | ”和谐方程“的根 |
| x2+6x+9=0 | x1=-3,x2=-3 | 9x2+6x+1=0 | x1=-$\frac{1}{3}$,x2=-$\frac{1}{3}$ |
| x2-5x+6=0 | x1=2,x2=3 | 6x2-5x+1=0 | x1=$\frac{1}{2}$,x2=$\frac{1}{3}$ |
| -$\frac{1}{6}$x2-$\frac{1}{6}$x+1=0 | x1=2,x2=-3 | x2-$\frac{1}{6}$x-$\frac{1}{6}$=0 | x1=$\frac{1}{2}$,x2=-$\frac{1}{3}$ |
| 2x2-3x-2=0 | x1=2,x2=-$\frac{1}{2}$ | -2x2-3x+2=0 | x1=$\frac{1}{2}$,x2=-2 |
(3)已知关于x的方程2016x2+bx-1=0的两根是x1=-1,x2=$\frac{1}{2016}$.请利用(2)中的结论,解关于x的方程:(x-1)2-bx+b=2016.
10.已知代数式-2xm-1y3与$\frac{5}{2}$xnym+n是同类项,则m,n的值是( )
| A. | $\left\{\begin{array}{l}m=2\\ n=-1\end{array}$ | B. | $\left\{\begin{array}{l}m=-2\\ n=-1\end{array}$ | C. | $\left\{\begin{array}{l}m=2\\ n=1\end{array}$ | D. | $\left\{\begin{array}{l}m=-2\\ n=1\end{array}$ |
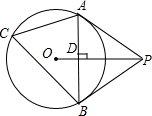 如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D.
如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D. 一棵树(AB)和一根木杆(CD)在同一时刻的投影如图所示,木杆CD高3米,影子DE长2米;若树的影子BE长6米,则树AB长多少米?
一棵树(AB)和一根木杆(CD)在同一时刻的投影如图所示,木杆CD高3米,影子DE长2米;若树的影子BE长6米,则树AB长多少米? 如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.
如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点. 如图,直径为1000mm的圆柱形水管有积水(阴影部分),水面的宽度AB为800mm,求水的最大深度CD.
如图,直径为1000mm的圆柱形水管有积水(阴影部分),水面的宽度AB为800mm,求水的最大深度CD. 如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米.
如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米.