题目内容
10.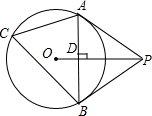 如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D.
如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D.(1)求证:PB为⊙O的切线;
(2)若tan∠BCA=$\frac{4}{3}$,⊙O的半径为10,求线段PD的长.
分析 (1)要证PB为⊙O的切线PB为⊙O的切线,只要证明△OAP≌△OBP即可,根据题目中的条件可以证明该结论成立;
(2)根据同弧所对的圆心角是圆周角的二倍,由tan∠BCA=$\frac{4}{3}$,⊙O的半径为10,可以得到OP和OD的长,从而可以解答本题.
解答  (1)证明:连接OA、OB,如右图所示,
(1)证明:连接OA、OB,如右图所示,
∵PA=PB,OA=OB,OP=OP,
∴△OAP≌△OBP(SSS),
∴∠OAP=∠OBP,
∵PA为⊙O的切线,
∴∠OAP=90°,
∴∠OBP=90°,
∴PB为⊙O的切线;
(2)解:∵△OAP≌△OBP,
∴∠AOP=∠BOP,
又∵∠AOB=2∠BCA=∠AOP+∠BOP,
∴∠BCA=∠AOP,
∵tan∠BCA=$\frac{4}{3}$,⊙O的半径为10,
∴tan∠AOP=$\frac{4}{3}$,OA=10,
∴AP=OA•tan∠AOP=10×$\frac{4}{3}$=$\frac{40}{3}$,OD=6,
∴OP=$\frac{50}{3}$,
∴PD=OP-OD=$\frac{32}{3}$.
点评 本题考查切线的性质、三角形的外接圆与外心、解直角三角形,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
2.一个数的平方根是2m-1和m+1,则这个数是( )
| A. | 2 | B. | -2 | C. | 4 | D. | 1 |
19.使分式$\frac{{{x^2}+1}}{1-3x}$的值为负的条件是( )
| A. | x<0 | B. | x>0 | C. | x>$\frac{1}{3}$ | D. | x<$\frac{1}{3}$ |
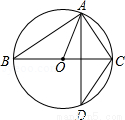

 已知,如图双曲线y=$\frac{4}{x}$(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=$\frac{2}{x}$(x>0)交于点C,点D,则:
已知,如图双曲线y=$\frac{4}{x}$(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=$\frac{2}{x}$(x>0)交于点C,点D,则: 如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是①③④.(填写序号)
如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是①③④.(填写序号)