题目内容
3.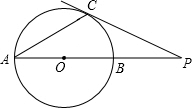 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则BP的长为$\sqrt{3}$.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则BP的长为$\sqrt{3}$.
分析 在RT△POC中,根据∠P=30°,PC=3,求出OC、OP即可解决问题.
解答 解: ∵OA=OC,∠A=30°,
∵OA=OC,∠A=30°,
∴∠OCA=∠A=30°,
∴∠COB=∠A+∠ACO=60°,
∵PC是⊙O切线,
∴∠PCO=90°,∠P=30°,
∵PC=3,
∴OC=PC•tan30°=$\sqrt{3}$,PO=2OC=2$\sqrt{3}$,
∴PB=PO-OB=$\sqrt{3}$,
故答案为$\sqrt{3}$.
点评 本题考查切线的性质、直角三角形中30度角所对的直角边等于斜边的一半,锐角三角函数等知识,解题的关键是利用切线的性质,在RT△POC解三角形是突破口,属于中考常考题型.

练习册系列答案
相关题目
11. 如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
 如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
如图,直线a、b被直线c所截,下列条件能使a∥b的是( )| A. | ∠1=∠6 | B. | ∠2=∠6 | C. | ∠1=∠3 | D. | ∠5=∠7 |
18.同时抛掷三枚质地均匀的硬币,至少有两枚硬币正面向上的概率是( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
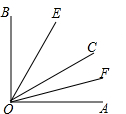 如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.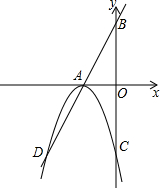 如图,直线AB解析式为y=2x+4,C(0,-4),AB交x轴于A,A为抛物线顶点,交y轴于C,
如图,直线AB解析式为y=2x+4,C(0,-4),AB交x轴于A,A为抛物线顶点,交y轴于C,