题目内容
20.下列运算正确的是( )| A. | a3•a4=a7 | B. | (3a-b)2=9a2-b2 | C. | (ab)3=ab3 | D. | 4a-3a=1 |
分析 根据同底数幂的乘法法则、完全平方公式以及积的乘方、合并同类项进行计算即可.
解答 解:A、a3•a4=a7,故A正确;
B、(3a-b)2=9a2-6a+b2,故B错误;
C、(ab)3=a3b3,故C错误;
D、4a-3a=a,故D错误;
故选A.
点评 本题考查了整式的混合运算,掌握同底数幂的乘法、完全平方公式以及积的乘方、合并同类项是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
11. 将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
 将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )| A. | 136° | B. | 138° | C. | 140° | D. | 142° |
18.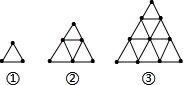 探索规律并填空
探索规律并填空
1+2=$\frac{2×(1+2)}{2}$;
1+2+3=$\frac{3×(1+3)}{2}$;
1+2+3+4=$\frac{4×(1+4)}{2}$;
1+2+3…+20=210;
1+2+3+…+n=$\frac{n(n+1)}{2}$.
用火柴棒按下面的方式搭图形填写表
照规律搭下去:
(1)第n个图形的大三角形周长的火柴棒是几根?
(2)第n个图形的小三角形个数有几个?第200个图形的小三角形个数有几个?
 探索规律并填空
探索规律并填空1+2=$\frac{2×(1+2)}{2}$;
1+2+3=$\frac{3×(1+3)}{2}$;
1+2+3+4=$\frac{4×(1+4)}{2}$;
1+2+3…+20=210;
1+2+3+…+n=$\frac{n(n+1)}{2}$.
用火柴棒按下面的方式搭图形填写表
| 图形编号 | ① | ② | ③ | ④ |
| 大三角形周长的火柴棒根数 | 3 | 6 | 9 | 12 |
| 小三角形个数 | 1 | 4 | 9 | 16 |
(1)第n个图形的大三角形周长的火柴棒是几根?
(2)第n个图形的小三角形个数有几个?第200个图形的小三角形个数有几个?
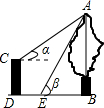 如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB=$\frac{3\sqrt{3}+12}{2}$(结果保留根号)
如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB=$\frac{3\sqrt{3}+12}{2}$(结果保留根号) 如图,直线l1∥l2,CD⊥AB于点D,∠1=44°,则∠2的度数为46°.
如图,直线l1∥l2,CD⊥AB于点D,∠1=44°,则∠2的度数为46°.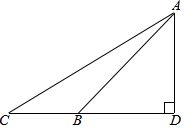 如图,长4m的楼梯AB的倾斜角∠ABD为45°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为30°,求调整后的楼梯AC的长.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,长4m的楼梯AB的倾斜角∠ABD为45°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为30°,求调整后的楼梯AC的长.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)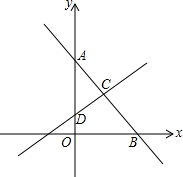 如图,直线AB分别与y轴,x轴交于点A(0,4)和点B(3,0),直线CD垂直平分线段AB交AB于点C,交y轴于点D.
如图,直线AB分别与y轴,x轴交于点A(0,4)和点B(3,0),直线CD垂直平分线段AB交AB于点C,交y轴于点D.