题目内容
11．若顺次连接某四边形四边中点所得的四边形是矩形，则原四边形一定是（ ）| A． | 菱形 | B． | 矩形 | C． | 对角线互相垂直 | D． | 对角线相等 |
分析 根据中位线的与对角线平行的性质，因此顺次连接四边中点可以得到一个相邻的边互相垂直的四边形，根据矩形的定义，邻边垂直的四边形为矩形．
解答 解：
当对角线互相垂直，即：四边形ABCD中，AC⊥BD时，
连接各边的中点E，F，G，H，
则形成中位线EG∥AC，FH∥AC，EF∥BD，GH∥BD，
又因为对角线AC⊥BD，
所以GH⊥EG，EG⊥EF，EF⊥FH，FH⊥HG，
根据矩形的定义可以判定该四边形为矩形．
故选C．
点评 本题考查的是矩形的判定定理（有一个角为直角的平行四边形为矩形），难度一般．
练习册系列答案
相关题目
1．下列各图，表示的数轴正确的是（ ）
| A． | （1） | B． | （2） | C． | （3） | D． | （4） |
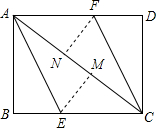如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处．
如图所示，在矩形ABCD中，E，F分别是边AB，CD上的点，AE=CF，连接EF，BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC．
3．在下列四个标志中，属于轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |