题目内容
6.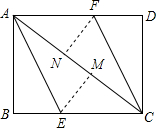 如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.(1)求证:四边形AECF是平行四边形;
(2)若AB=3,AC=5,求四边形AECF的面积.
分析 (1)首先证明△ABE≌△CDF,则DF=BE,然后可得到AF=EC,依据一组对边平行且相等四边形是平行四边形可证明AECF是平行四边形;
(2)由AB=3,AC=5,可得BC=4,设CE=x,则EM=4-x,CM=5-3=2,在Rt△CEM中,利用勾股定理可解得x,由平行四边形的面积公式可得结果.
解答 解:(1)∵四边形ABCD为矩形,
∴AB=CD,AD∥BC,∠B=∠D=90°,∠BAC=∠DCA.
由翻折的性质可知:∠EAB=$\frac{1}{2}$∠BAC,∠DCF=$\frac{1}{2}$∠DCA.
∴∠EAB=∠DCA.
在△ABE和△CDF中$\left\{\begin{array}{l}{∠B=∠D}\\{AB=CD}\\{∠EAB=∠DCA}\end{array}\right.$,
∴△ABE≌△CDF,
∴DF=BE.
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形;
(2)∵AB=3,AC=5,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=4,
设CE=x,则EM=4-x,CM=5-3=2,
在Rt△CEM中,依据勾股定理得:(4-x)2+22=x2,
解得:x=2.5,
∴四边形AECF的面积的面积为:EC•AB=2.5×3=7.5.
点评 本题主要考查了折叠的性质、矩形的性质、平行四边形的判定定理和勾股定理等,综合运用各定理是解答此题的关键.

练习册系列答案
相关题目
17.若△ABC内接于⊙O,∠BOC=130°,则∠A的度数为( )
| A. | 50° | B. | 50°或130° | C. | 65° | D. | 65°或115° |
1.用配方法解方程x2+4x=-2下列配方正确的是( )
| A. | (x+4)2=14 | B. | (x+2)2=6 | C. | (x+2)2=2 | D. | (x-2)2=2 |
11.若顺次连接某四边形四边中点所得的四边形是矩形,则原四边形一定是( )
| A. | 菱形 | B. | 矩形 | C. | 对角线互相垂直 | D. | 对角线相等 |
18. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得
BE=20m,EC=10m,CD=20m,则河的宽度AB=( )
 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB=( )
| A. | 60 m | B. | 40 m | C. | 30 m | D. | 20 m |
15.若x<y,则下列不等式中成立的是( )
| A. | 2+x>2+y | B. | 2x>2y | C. | 2-x>2-y | D. | -2x<-2y |