题目内容
20.某商店购进一批季节性小家电,单价40元.原定价为52元,每天可售出180个.如果定价每增加1元,销售量将减少10个.(利润=售价-进价)该商场为了确定更合理的销售价格,作了如下测算:(1)按原定价销售,每天可获利润2160元;
(2)若销售价为59元,每天可售出110个,每天可获利润2090元;
(3)如果定价增加x元(x为整数),
①每天可售出180-10x个(用代数式表示);
②每天可获利润-10x2+60x+2160元(用代数式表示);
③当x=3时,每天可获得的最大利润为2250元.
分析 (1)根据单件的利润乘以销售的数量等于利润,可得答案;
(2)根据单件的利润乘以销售的数量等于利润,可得答案;
(3)①根据原来的数量减减少的数量,可得答案;②根据单件的利润乘以销售的数量等于利润,可得答案;③根据二次函数的性质,可得答案.
解答 解:(1)按原定价销售,每天可获利润 2160元;
(2)若销售价为59元,每天可售出 110个,每天可获利润 2090元;
(3)如果定价增加x元(x为整数),
①每天可售出 180-10x个(用代数式表示);
②每天可获利润-10x2+60x+2160元(用代数式表示);
③当x=3时,每天可获得的最大利润为 2250元,
故答案为:2160;110,2090;180-10x,-10x2+60x+2160,3,2250.
点评 本题考查了列代数式,利用单件的利润乘以销售的数量等于利润.

练习册系列答案
相关题目
11.若顺次连接某四边形四边中点所得的四边形是矩形,则原四边形一定是( )
| A. | 菱形 | B. | 矩形 | C. | 对角线互相垂直 | D. | 对角线相等 |
15.若x<y,则下列不等式中成立的是( )
| A. | 2+x>2+y | B. | 2x>2y | C. | 2-x>2-y | D. | -2x<-2y |
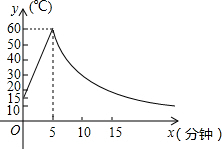 制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图所示).已知该材料在操作加热前的温度为15℃,加热5min后温度达到60℃.
制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图所示).已知该材料在操作加热前的温度为15℃,加热5min后温度达到60℃.
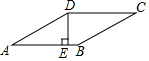 如图,菱形ABCD的高DE是5cm,∠A:∠B=1:5,求∠A的度数及菱形ABCD的面积.
如图,菱形ABCD的高DE是5cm,∠A:∠B=1:5,求∠A的度数及菱形ABCD的面积.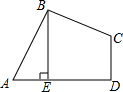 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE等于2.
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE等于2.