题目内容
17.(1)因式分解:6x3-x2-x=x(3x+1)(2x-1)(2)因式分解:x2+3x(x-3)-9=(x-3)(4x+3).
分析 (1)原式提取x,再利用十字相乘法分解即可;
(2)原式第一、三项结合后,利用平方差公式分解,再提取公因式即可.
解答 解:(1)原式=x(6x2-x-1)=x(3x+1)(2x-1);
(2)原式=(x+3)(x-3)+3x(x-3)=(x-3)(4x+3),
故答案为:(1)x(3x+1)(2x-1);(2)(x-3)(4x+3)
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
7.用科学记数法表示0.000625,正确的是( )
| A. | 6.25×10-4 | B. | 625×10-6 | C. | 6.25×10-6 | D. | 0.625×10-3 |
7.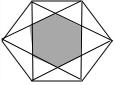 如图,边长为a的正六边形中,连接一些顶点,中间围成一个新的小正六边形(阴影部分),则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$(l为周长)等于( )
如图,边长为a的正六边形中,连接一些顶点,中间围成一个新的小正六边形(阴影部分),则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$(l为周长)等于( )
 如图,边长为a的正六边形中,连接一些顶点,中间围成一个新的小正六边形(阴影部分),则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$(l为周长)等于( )
如图,边长为a的正六边形中,连接一些顶点,中间围成一个新的小正六边形(阴影部分),则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$(l为周长)等于( )| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 2 |
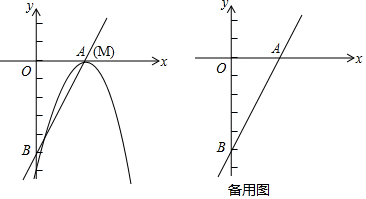
 一次函数y=kx+b的图象如图所示,当x>0时,y的取值范围为y>-4.
一次函数y=kx+b的图象如图所示,当x>0时,y的取值范围为y>-4.