题目内容
10. 已知:AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:BC=EF.
已知:AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:BC=EF.
分析 根据平行线的性质得出∠A=∠EDF,∠F=∠BCA,再利用等式的性质得出AC=DF,进而证明三角形全等解答即可.
解答 证明:∵AB∥DE,BC∥EF,
∴∠A=∠EDF,∠F=∠BCA,
∵AD=CF,
∴AC=DF,
在△ABC与△DEF中,
$\left\{\begin{array}{l}{∠A=∠EDF}\\{AC=DF}\\{∠F=∠BCA}\end{array}\right.$,
∴△ABC≌△DEF(ASA),
∴BC=EF.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA和HL,做题时,要根据已知条件结合图形进行思考.

练习册系列答案
相关题目
18.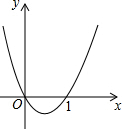 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②a<0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②a<0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②a<0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②a<0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )| A. | ①④ | B. | ②③④ | C. | ③④⑤ | D. | ①③⑤ |
5.下列分式$\frac{1}{{(x-1{)^2}}}$,$\frac{1}{{{x^2}+1}}$,$\frac{5}{x-1}$的最简公分母为( )
| A. | (x2+1)(x-1) | B. | (x-1)2 | C. | (x-1)2(x2+1) | D. | (x2-1)(x2+1) |
 美国圣路易斯市有一座巨大的拱门,这座拱高和底宽都是192m的不锈钢拱门是美国开发西部的标志性建筑.如果把拱门看作一条抛物线,试建立恰当的平面直角坐标系,并写出与该抛物线相应的函数表达式.
美国圣路易斯市有一座巨大的拱门,这座拱高和底宽都是192m的不锈钢拱门是美国开发西部的标志性建筑.如果把拱门看作一条抛物线,试建立恰当的平面直角坐标系,并写出与该抛物线相应的函数表达式.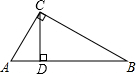 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=3,BD=8,则CD=2$\sqrt{6}$.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=3,BD=8,则CD=2$\sqrt{6}$. 已知抛物线y=x2-2x-3.
已知抛物线y=x2-2x-3.