题目内容
1. 美国圣路易斯市有一座巨大的拱门,这座拱高和底宽都是192m的不锈钢拱门是美国开发西部的标志性建筑.如果把拱门看作一条抛物线,试建立恰当的平面直角坐标系,并写出与该抛物线相应的函数表达式.
美国圣路易斯市有一座巨大的拱门,这座拱高和底宽都是192m的不锈钢拱门是美国开发西部的标志性建筑.如果把拱门看作一条抛物线,试建立恰当的平面直角坐标系,并写出与该抛物线相应的函数表达式.
分析 以拱门底部中点为原点,水平面为x轴,竖直方向为y轴建立坐标系,设抛物线相应的函数表达式:y=ax2+192,代入点的坐标,即可得到结论.
解答  解:如图,以拱门底部中点为原点,水平面为x轴,竖直方向为y轴建立坐标系,
解:如图,以拱门底部中点为原点,水平面为x轴,竖直方向为y轴建立坐标系,
设抛物线相应的函数表达式:y=ax2+192,
∵该抛物线过点B(96,0),
∴0=962a+192 解得a=-$\frac{1}{48}$,
∴拱桥对应的二次函数解析式为:y=-$\frac{1}{48}$x2+192.
点评 此题考查二次函数的实际运用,利用待定系数法求函数解析式,建立函数与方程之间的联系是解决问题的关键.

练习册系列答案
相关题目
14. 如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,OP=8,则⊙O的半径( )
如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,OP=8,则⊙O的半径( )
 如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,OP=8,则⊙O的半径( )
如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,OP=8,则⊙O的半径( )| A. | 4 | B. | 2$\sqrt{7}$ | C. | 5 | D. | 10 |
11.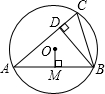 如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
 如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )| A. | OM的长 | B. | $\frac{1}{2}$OM的长 | C. | 2OM的长 | D. | CD的长 |
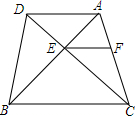 如图,在四边形ABCD中,CD交AB于点E,且AE:EB=1:2,EF∥BC∥AD,EF交AC于点F,S△ADE=1,求S△AEF和S△BCE.
如图,在四边形ABCD中,CD交AB于点E,且AE:EB=1:2,EF∥BC∥AD,EF交AC于点F,S△ADE=1,求S△AEF和S△BCE.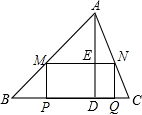 在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y.
在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y. 已知:AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:BC=EF.
已知:AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:BC=EF.