题目内容
6．已知3x2-mx+3=（x-1）（3x+n），求（m-n）2的值．分析 已知等式右边利用多项式乘以多项式法则计算，利用多项式相等的条件求出m与n的值，代入原式计算即可得到结果．
解答 解：3x2-mx+3=（x-1）（3x+n）=3x2+（n-3）x-n，
∴-m=n-3，-n=3，
解得：m=6，n=-3，
则原式=81．
点评 此题考查了因式分解-十字相乘法，熟练掌握十字相乘的方法是解本题的关键．
练习册系列答案
相关题目
17．已知菱形ABCD，∠A等于120°，AB=6，E为AB的中点，F、M分别在AD、DC上滑动，且FM=3，则△FME面积的最大值为（ ）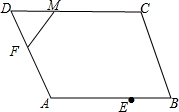 
| A． | 12 | B． | 6 | C． | $\frac{7}{4}$$\sqrt{3}$ | D． | $\frac{9}{2}$$\sqrt{3}$ |
14．在△ABC中，点D在AB上，点E在AC上，且DE∥BC，$\frac{AD}{DB}$=$\frac{4}{5}$，则$\frac{EC}{AC}$=（ ）
| A． | $\frac{9}{5}$ | B． | $\frac{5}{4}$ | C． | $\frac{5}{9}$ | D． | $\frac{4}{9}$ |
如图，一个矩形广场的长为60m，宽为40m，广场内两条纵向小路的宽均为1.5m，如果设两条横向小路的宽都为x m，那么当x为多少时，小路内外边缘所围成的两个矩形相似？
18．检验下列各方程的解正确的是（ ）
| A． | 2x-1=$\frac{2}{3}-3x（x=\frac{1}{3}）$ | B． | 1=$\frac{x}{2}-4$（x=-10） | ||
| C． | 4x+2=-x-3（x=1） | D． | 0.48x-6=0.02x（x=1.2） |
15．已知$\frac{a}{2}$=$\frac{b}{3}$≠0，则$\frac{a+2b}{b}$的值为（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{5}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |