题目内容
 如图,点C在线段AB上,BC=2AC,M、N是AC、BC中点,若AB=a,求BC-MN.
如图,点C在线段AB上,BC=2AC,M、N是AC、BC中点,若AB=a,求BC-MN.考点:两点间的距离
专题:
分析:先根据BC=2AC,AB=a求出AC及BC的长,再根据M、N是AC、BC中点可得出MC及NC的长,进而可得出结论.
解答:解:∵BC=2AC,AB=a,
∴BC=
a,AC=
a,
∵M、N是AC、BC中点,
∴MC=
AC=
a,NC=
BC=
a,
∴MN=MC+NC=
a+
a=
a,
∴BC-MN=
a-
a=
a.
∴BC=
| 2 |
| 3 |
| 1 |
| 3 |
∵M、N是AC、BC中点,
∴MC=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
∴MN=MC+NC=
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
∴BC-MN=
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为( )
如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为( )| A、30° | B、50° |
| C、90° | D、100° |
 梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:
梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法: 如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与x轴的交点.
如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与x轴的交点. 如图,BM、CN是△ABC的角平分线,AE⊥BM于E,AF⊥CN于F.求证:EF∥BC.
如图,BM、CN是△ABC的角平分线,AE⊥BM于E,AF⊥CN于F.求证:EF∥BC.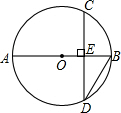 如图,AB为⊙O的直径,弦CD⊥AB于E,已知AB=20,EB=2,求CD的长.
如图,AB为⊙O的直径,弦CD⊥AB于E,已知AB=20,EB=2,求CD的长.