题目内容
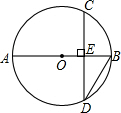如图，AB为⊙O的直径，弦CD⊥AB于E，已知AB=20，EB=2，求CD的长．考点：垂径定理,勾股定理
专题：
分析：连接OC，求出OC、OE，根据垂径定理求出CD=2CE，根据勾股定理求出CE即可．
解答：
解：连接OC，
∵AB=20，EB=2，
∴AO=OB=OC=10，OE=8，
∵AB⊥CD，
∴CD=2CE，∠CEO=90°，
由勾股定理得：CE=
=
=6，
∴CD=12．
解：连接OC，∵AB=20，EB=2，
∴AO=OB=OC=10，OE=8，
∵AB⊥CD，
∴CD=2CE，∠CEO=90°，
由勾股定理得：CE=
| OC2-OE2 |
| 102-82 |
∴CD=12．
点评：本题考查了垂径定理和勾股定理的应用，解此题的关键是求出CE长和得出CD=2CE．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
如图，点C在线段AB上，BC=2AC，M、N是AC、BC中点，若AB=a，求BC-MN．
如图，四边形ABCD内接于⊙O，延长AD、BC相交于点M，延长AB、DC相交于点N，∠M=40°，∠N=20°，求∠A的度数．
如图为直径20cm的圆柱形油槽，装入油后，油深CD为8cm，那么油面宽度AB=弦心距为4，弦长为8的弦所对的劣弧长是（ ）
A、
| ||
| B、4π | ||
C、2
| ||
| D、8π |
如图，四边形ABC内接于⊙O，若∠C=150°，则∠A=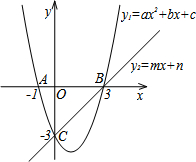
如图，在同一直角坐标系中，抛物线y1=ax2+bx+c与两坐标轴分别交于A（-1，0）、点B（3，0）和点C（0，-3），直线y2=mx+n与抛物线交于B、C两点．