题目内容
2.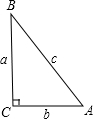 已知:如图,直角三角形BCA中,∠BCA=90°,BC=a,CA=b,AB=c,请你用两种方法证明:a2+b2=c2.
已知:如图,直角三角形BCA中,∠BCA=90°,BC=a,CA=b,AB=c,请你用两种方法证明:a2+b2=c2.
分析 方法1:根据“4个小直角三角形的面积=大正方形的面积-小正方形的面积”进行证明.
方法2:首先连结AD,过点A作DE边上的高BF,则AF=a-b,表示出S五边形BCAED,进而得出答案.
解答 解:方法1:如图所示: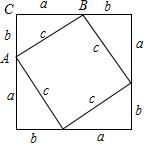
4S△ABC=S大正方形-S小正方形,即4×$\frac{1}{2}$ab=(a+b)2-c2,
所以a2+b-c2=0,即a2+b2=c2.
方法2:连结AD,过点A作DE边上的高AF,则AF=a-b.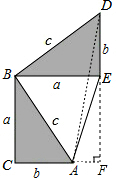
∵S五边形BCAED=S△ACB+S△ABE+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$a2+$\frac{1}{2}$ab,
又∵S五边形ACBED=S△ACB+S△ABD+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$b(a-b),
∴$\frac{1}{2}$ab+$\frac{1}{2}$a2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$b(a-b),
∴a2+b2=c2.
点评 本题考查了勾股定理的应用,解题时是用数形结合来证明勾股定理,锻炼了同学们的数形结合的思想方法.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
17.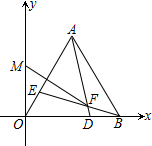 如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )
如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )
 如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )
如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )| A. | 3 | B. | $\sqrt{3}$+1 | C. | 2$\sqrt{3}$-2 | D. | 6-2$\sqrt{3}$ |

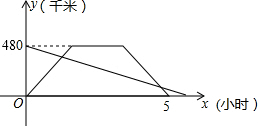 一辆动车和一辆普快分别从A、B两地同时出发相向而行,动车到达B地停留1小时后原速返回A地,结果比普快早1小时到达A地,它们离A地的路程随时间变化的图象如图所示,则下列结论中正确的个数是( )
一辆动车和一辆普快分别从A、B两地同时出发相向而行,动车到达B地停留1小时后原速返回A地,结果比普快早1小时到达A地,它们离A地的路程随时间变化的图象如图所示,则下列结论中正确的个数是( )
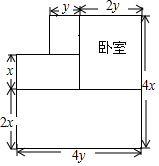 如图,是张老师买的经济适用房平面结构示意图,图中标明了有关尺寸(墙体厚度忽略不计,单位:m),房主计划把卧室以外的地面都铺上地砖,
如图,是张老师买的经济适用房平面结构示意图,图中标明了有关尺寸(墙体厚度忽略不计,单位:m),房主计划把卧室以外的地面都铺上地砖,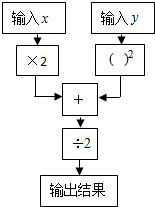 求代数式的值:
求代数式的值: