题目内容
14.在△ABC中,点D,E分别在边AB,AC上,△ADE∽△ABC,如果AB=4,BC=5,AC=6,AD=3,那么△ADE的周长为$\frac{45}{4}$.分析 根据题意画出图形,根据相似三角形的性质求出DE及AE的长,进而可得出结论.
解答 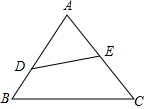 解:如图,∵△ADE∽△ABC,
解:如图,∵△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$,即$\frac{3}{4}$=$\frac{DE}{5}$=$\frac{AE}{6}$,解得DE=$\frac{15}{4}$,AE=$\frac{9}{2}$,
∴△ADE的周长=AD+AE+DE=3+$\frac{9}{2}$+$\frac{15}{4}$=$\frac{45}{4}$;
故答案为:$\frac{45}{4}$.
点评 本题考查的是相似三角形的性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
相关题目
5.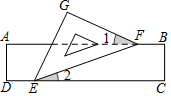 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是( )
 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是( )| A. | 30° | B. | 23° | C. | 20° | D. | 15° |

 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴的正半轴相交于点A,与y轴相交于点B,点C在线段OA上,点D在此抛物线上,CD⊥x轴,且∠DCB=∠DAB,AB与CD相交于点E.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴的正半轴相交于点A,与y轴相交于点B,点C在线段OA上,点D在此抛物线上,CD⊥x轴,且∠DCB=∠DAB,AB与CD相交于点E.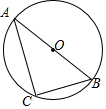 如图,AB是⊙O的直径,点C在圆上,且∠ABC=50°,则∠BAC=40°.
如图,AB是⊙O的直径,点C在圆上,且∠ABC=50°,则∠BAC=40°.