题目内容
2.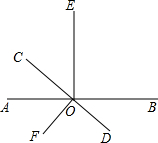 如图,直线AB与CD相交于D,OE⊥AB,OF⊥CD,
如图,直线AB与CD相交于D,OE⊥AB,OF⊥CD,(1)图中与∠COE互补的角是∠DOE、∠BOF;(把符合条件的角都写出来)
(2)如果∠AOC=$\frac{2}{7}$∠EOF,求∠AOC的度数.
分析 (1)根据角的互补性质,即可得到.
(2)先设出∠AOC=x°,根据互补角的和为180°,解方程即可得出答案.
解答 解:(1)∵∠COE+∠DOE=180°,∠DOE=BOF,
∴与∠COE互补的角是∠DOE、∠BOF.
故答案为:∠DOE、∠BOF;
(2)设∠AOC=x°,则∠EOF=$\frac{7}{2}$x°,
∵OE⊥AB,OF⊥CD,
∴∠AOE=∠COF=90°;
∴∠COE=90°-x°,
∴∠EOF=(90°-x°)+90°=180°-x°;
又∵∠EOF=$\frac{7}{2}$x°,
∴180°-x°=$\frac{7}{2}$x°;
解得x=40.
即∠AOC=40°.
点评 本题考查了垂线的定义,余角和补角,正确掌握余角的性质和补角的性质是解题的关键.

练习册系列答案
相关题目
11. 如图,a∥b,∠3+∠4=110°,则∠1+∠2的度数为( )
如图,a∥b,∠3+∠4=110°,则∠1+∠2的度数为( )
 如图,a∥b,∠3+∠4=110°,则∠1+∠2的度数为( )
如图,a∥b,∠3+∠4=110°,则∠1+∠2的度数为( )| A. | 60° | B. | 70° | C. | 90° | D. | 110° |
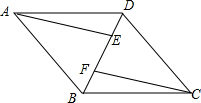 已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.