题目内容
7.求下列各抛物线的解析式:(1)已知一条抛物线的顶点在y轴上,且经过(1,-2),(2,3)两点;
(2)已知某抛物线与抛物线y=2x2+3的形状、开口方向都一样,顶点为(0,4);
(3)已知抛物线y=ax2+c与x轴交于两点(2,0),(-2,0),与y轴交于点(0,2)
分析 (1)设抛物线的解析式是y=ax2+k,把(1,-2),(2,3)代入得出方程组,求出方程组的解即可;
(2)根据抛物线的形状开口方向和抛物线的形状与a值有关,利用顶点式解析式写出即可;
(3)把点(2,0)和(0,2)代入求出即可.
解答 解:(1)∵抛物线的顶点在y轴上,
∴设抛物线的解析式是y=ax2+k,
把(1,-2),(2,3)代入得:$\left\{\begin{array}{l}{a+k=-2}\\{4a+k=3}\end{array}\right.$,
解得:a=$\frac{5}{3}$,k=-$\frac{11}{3}$.
即抛物线的解析式是y=$\frac{5}{3}$x2-$\frac{11}{3}$;
(2)∵抛物线的顶点坐标(0,4),形状开口方向与抛物线y=2x2+3相同,
∴这个二次函数的解析式为y=2(x-0)2+4,即y=2x2+4;
抛物线y=ax2+c与x轴交于两点(2,0),(-2,0),与y轴交于点(0,2)
(3)∵抛物线y=ax2+c与x轴交于两点(2,0),(-2,0),与y轴交于点(0,2),
∴代入得:$\left\{\begin{array}{l}{4a+c=0}\\{c=2}\end{array}\right.$,
解得:a=-$\frac{1}{2}$,c=2,
即抛物线的解析式是y=-$\frac{1}{2}$x2+2.
点评 本题考查了二次函数图象与几何变换的应用,能正确设解析式是解此题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
18.下列二次根式:①$\sqrt{12}$②$\sqrt{0.5}$③$\sqrt{\frac{2}{3}}$④$\sqrt{27}$中,与$\sqrt{3}$是同类二次根式的是( )
| A. | ①和③ | B. | ②和③ | C. | ①和④ | D. | ③和④ |
15.下列不是同类项的是( )
| A. | 0与$\frac{1}{2}$ | B. | 5x与2y | C. | -$\frac{1}{4}$a2b与3a2b | D. | -2x2y2与$\frac{1}{2}$x2y2 |
12.4的平方根是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | ±$\sqrt{2}$ |
17.正比例函数y=(2k+1)x,若y随x增大而减小,则k的取值范围是( )
| A. | k>-$\frac{1}{2}$ | B. | k<-$\frac{1}{2}$ | C. | k=$\frac{1}{2}$ | D. | k=0 |
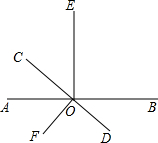 如图,直线AB与CD相交于D,OE⊥AB,OF⊥CD,
如图,直线AB与CD相交于D,OE⊥AB,OF⊥CD,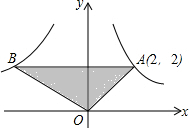 如图,点A(2,2)是反比例函数y=$\frac{m}{x}$(x>0)的图象上一点,点B是反比例函数y=$\frac{n}{x}$(x<0)上一点,AB与x轴平行,且△OAB的面积为5,则m+n=-2.
如图,点A(2,2)是反比例函数y=$\frac{m}{x}$(x>0)的图象上一点,点B是反比例函数y=$\frac{n}{x}$(x<0)上一点,AB与x轴平行,且△OAB的面积为5,则m+n=-2.