题目内容
12.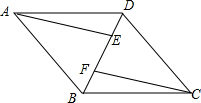 已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
分析 (1)利用平行四边形的性质结合全等三角形的判定方法(AAS),得出即可;
(2)利用全等三角形的性质得出AE=CF,进而求出四边形AFCE是平行四边形,再利用菱形的判定方法得出答案.
解答 证明:(1)如图:
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠1=∠2,
∵AE∥CF,
∴∠3=∠4,
在△AEB和△CFD中,
$\left\{\begin{array}{l}∠3=∠4\\∠1=∠2\\ AB=CD\end{array}\right.$,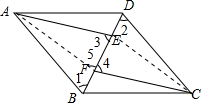
∴△AEB≌△CFD(AAS);
(2)∵△AEB≌△CFD,
∴AE=CF,
∵AE∥CF,
∴四边形AFCE是平行四边形.
∵∠5=∠4,∠3=∠4,
∴∠5=∠3.
∴AF=AE.
∴四边形AFCE是菱形.
点评 此题主要考查了平行四边形的性质以及菱形的判定和全等三角形的判定与性质,正确利用全等三角形的判定与性质是解题关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
20.下列图案中,既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.正比例函数y=(2k+1)x,若y随x增大而减小,则k的取值范围是( )
| A. | k>-$\frac{1}{2}$ | B. | k<-$\frac{1}{2}$ | C. | k=$\frac{1}{2}$ | D. | k=0 |
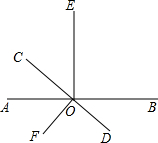 如图,直线AB与CD相交于D,OE⊥AB,OF⊥CD,
如图,直线AB与CD相交于D,OE⊥AB,OF⊥CD,
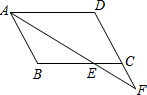 在?ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,$\frac{AE}{EF}$=2,CF=3.求CD,AD的长.
在?ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,$\frac{AE}{EF}$=2,CF=3.求CD,AD的长.


