题目内容
13.已知A、B为数轴上的两点,两点A、B对应的数分别为-5和4,点P为线段AB的三等分点(点P靠近A点),则点P所对应的数是-2.分析 首先根据线段的长度的求法,求出AB的长度是多少,进而求出AP的长度是多少;然后用AP的长度加上点A对应的数,求出点P所对应的数是多少即可.
解答 解:[4-(-5)]÷3+(-5)
=9÷3+(-5)
=3-5
=-2,
即点P所对应的数是-2.
故答案为:-2.
点评 (1)此题主要考查了数轴的特征和应用,要熟练掌握,解答此题的关键是要明确:所有的有理数都可以用数轴上的点表示,但数轴上的点不都表示有理数.(一般取右方向为正方向,数轴上的点对应任意实数,包括无理数.
(2)此题还考查了线段的长度的求法,要熟练掌握,解答此题的关键是求出AP的长度是多少.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
7.下列分式运算或化简错误的是( )
| A. | $\frac{1-3x}{-x-2}$=$\frac{3x-1}{x+2}$ | B. | $\frac{-2{x}^{3}y}{4{x}^{2}{y}^{2}}$=-$\frac{x}{2y}$ | ||
| C. | (x2-xy)÷$\frac{x-y}{x}$=(x-y)2 | D. | $\frac{4}{x-2}$+$\frac{x+2}{2-x}$=-1 |
18.下列二次根式:①$\sqrt{12}$②$\sqrt{0.5}$③$\sqrt{\frac{2}{3}}$④$\sqrt{27}$中,与$\sqrt{3}$是同类二次根式的是( )
| A. | ①和③ | B. | ②和③ | C. | ①和④ | D. | ③和④ |
5. 如图,AB、CD交于点O,OE⊥AB,则∠1与∠2一定满足关系是( )
如图,AB、CD交于点O,OE⊥AB,则∠1与∠2一定满足关系是( )
 如图,AB、CD交于点O,OE⊥AB,则∠1与∠2一定满足关系是( )
如图,AB、CD交于点O,OE⊥AB,则∠1与∠2一定满足关系是( )| A. | 对顶角 | B. | 相等 | C. | 互补 | D. | 互余 |
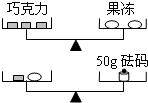 列方程解应用题:如图所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,求每一块巧克力的质量是多少.
列方程解应用题:如图所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,求每一块巧克力的质量是多少.
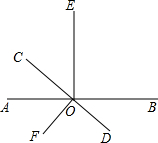 如图,直线AB与CD相交于D,OE⊥AB,OF⊥CD,
如图,直线AB与CD相交于D,OE⊥AB,OF⊥CD,