题目内容
12.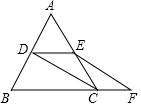 如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.
如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.
分析 欲证明四边形CDEF是平行四边形,只需推知DE∥CF,DE=CF;
解答 证明:∵在△ABC中,D、E分别是边AB、AC的中点,
∴DE∥BC且DE=$\frac{1}{2}$BC.
又∵CF=$\frac{1}{2}$BC,
∴DE=CF,
∴四边形DEFC是平行四边形.
点评 本题考查了平行四边形的判定与性质、三角形中位线定理;熟练掌握三角形中位线定理是解决问题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
2.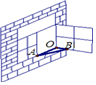 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )| A. | 垂线段最短 | B. | 两点之间线段最短 | ||
| C. | 两点确定一条直线 | D. | 三角形的稳定性 |
4.为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13-10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
(1)该市规定用水量为8吨,规定用量内的收费标准是2元/吨,超过部分的收费标准是3元/吨.
(2)若小明家五月份用水20吨,则应缴水费52元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
| 月份 | 一 | 二 | 三 | 四 |
| 用水量(吨) | 6 | 7 | 12 | 15 |
| 水费(元) | 12 | 14 | 28 | 37 |
(2)若小明家五月份用水20吨,则应缴水费52元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
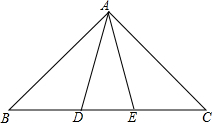 如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.
如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE. 如图,在矩形ABCD中,AB=2,∠ADB=30°,沿对角线BD折叠,使△ABD和△EBD落在同一平面内,则A,E之间的距离为2.
如图,在矩形ABCD中,AB=2,∠ADB=30°,沿对角线BD折叠,使△ABD和△EBD落在同一平面内,则A,E之间的距离为2.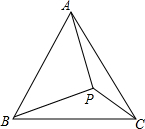 如图,P为等边三角形ABC内一点,PC=3,PA=4,PB=5,求∠APC的度数.
如图,P为等边三角形ABC内一点,PC=3,PA=4,PB=5,求∠APC的度数.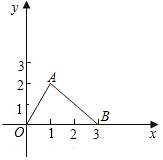 如图,在平面直角坐标系中,点A在第一象限,点A的横坐标为1,OA=2,求点A的坐标.
如图,在平面直角坐标系中,点A在第一象限,点A的横坐标为1,OA=2,求点A的坐标.