题目内容
17.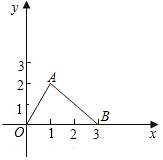 如图,在平面直角坐标系中,点A在第一象限,点A的横坐标为1,OA=2,求点A的坐标.
如图,在平面直角坐标系中,点A在第一象限,点A的横坐标为1,OA=2,求点A的坐标.
分析 过A作AC⊥x轴于C,根据勾股定理即可得到结论.
解答 解: 过A作AC⊥x轴于C,
过A作AC⊥x轴于C,
∵点A的横坐标为1,
∴OC=1,
∵OA=2,
∴AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=$\sqrt{3}$,
∴点A的坐标是(1,$\sqrt{3}$).
点评 本题考查了坐标与图形的性质,勾股定理,正确的理解题意是解题的关键.

练习册系列答案
相关题目
2.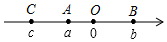 如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a-c=b;④$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$=1.其中正确的个数有( )
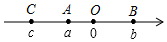 如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:①abc<0;②a(b+c)>0;③a-c=b;④$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$=1.其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.抛物线y=x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
则抛物线的解析式是y=x2-4x+3.
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
6.如图,直线AB,CD相交于点O,OT⊥AB于O,CE∥AB交CD于点C,若∠ECO=35°,则∠DOT=( )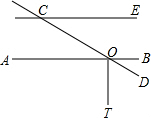

| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
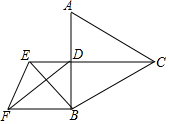 如图,等边三角形ABC的边长为8,CD⊥AB于点D,E为射线CD上一点,以BE为边在BE左侧作等边三角形BEF,求DF的最小值.
如图,等边三角形ABC的边长为8,CD⊥AB于点D,E为射线CD上一点,以BE为边在BE左侧作等边三角形BEF,求DF的最小值.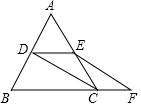 如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.
如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.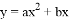 的图象如图,若一元二次方程
的图象如图,若一元二次方程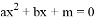 有实数根,则以下关于
有实数根,则以下关于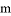 的结论正确的是( )
的结论正确的是( )