题目内容
17.观察下列各式:①$\sqrt{2+\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$; ②$\sqrt{3+\frac{3}{8}}$=3$\sqrt{\frac{3}{8}}$;③$\sqrt{4+\frac{4}{15}}$=4$\sqrt{\frac{4}{15}}$;…①当n≥2时,你发现了什么规律?用含有n的式子表示为$\sqrt{n+\frac{n}{{n}^{2}-1}}=n\sqrt{\frac{n}{{n}^{2}-1}}$.
②请用所学数学知识证明你的结论.
分析 利用二次根式的性质化简求出即可,进而得出规律求出答案.
解答 解:$\sqrt{2+\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$; ②$\sqrt{3+\frac{3}{8}}$=3$\sqrt{\frac{3}{8}}$;③$\sqrt{4+\frac{4}{15}}$=4$\sqrt{\frac{4}{15}}$;…
①当n≥2时,用含有n的式子表示为$\sqrt{n+\frac{n}{{n}^{2}-1}}=n\sqrt{\frac{n}{{n}^{2}-1}}$.
②$\sqrt{n+\frac{n}{{n}^{2}-1}}$
=$\sqrt{\frac{n({n}^{2}-1)}{{n}^{2}-1}+\frac{n}{{n}^{2}-1}}$
=$\sqrt{\frac{n({n}^{2}-1+1)}{{n}^{2}-1}}$
=$\sqrt{\frac{{n}^{2}•n}{{n}^{2}-1}}$
=n$\sqrt{\frac{n}{{n}^{2}-1}}$.
故答案为:$\sqrt{n+\frac{n}{{n}^{2}-1}}=n\sqrt{\frac{n}{{n}^{2}-1}}$.
点评 此题主要考查了二次根式的性质与化简,正确掌握二次根式的性质是解题关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(2,2)处,两直角边分别与坐标轴交于点A、B,则OA+OB的值为4.
如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(2,2)处,两直角边分别与坐标轴交于点A、B,则OA+OB的值为4.
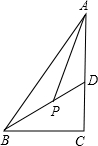 如图,在△ABC中,∠C=90°,∠BAC=30°,BD平分∠ABC,交AC于点D,AP平分∠BAC,交BD于点P,试求∠APD的度数.
如图,在△ABC中,∠C=90°,∠BAC=30°,BD平分∠ABC,交AC于点D,AP平分∠BAC,交BD于点P,试求∠APD的度数.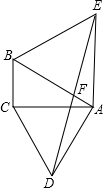 如图,在△ABC中,∠BCA=90°,∠BAC=30°,分别以AB、AC为边作等边三角形ABE和等边三角形ACD,连接ED交AB于点F.求证:
如图,在△ABC中,∠BCA=90°,∠BAC=30°,分别以AB、AC为边作等边三角形ABE和等边三角形ACD,连接ED交AB于点F.求证: