Question

7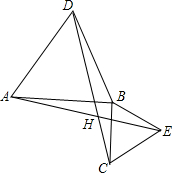．如果两个等边三角形△ABD和△BCE，连接AE与CD，证明：
（1）AE与DC的夹角为60°；
（2）AE与DC的交点设为H，BH平分∠AHC．

Answer 1

分析 （1）根据等边三角形性质得出AB=BD，BC=BE，∠ABD=∠CBE=60°，求出∠ABE=∠DBC．根据SAS证△ABE≌△DBC，则∠BDC=∠BAE，根据三角形的内角和定理可求出∠AHD=60°；
（2）过点B分别作BM⊥CD，NN⊥AE，垂足为点M，N．根据三角形的面积公式求出AN=AM，根据角平分线性质求出即可．

解答 证明：（1）∵△ABD和△BCE是等边三角形，
∴AB=BD，BC=BE，∠ABD=∠CBE=60°，
∴∠ABE=∠DBC，
在△ABE和△DBC中，
$\left\{\begin{array}{l}{AB=BD}\\{∠ABE=∠DBC}\\{BC=BE}\end{array}\right.$，
∴△ABE≌△DBC，
∴AE=DC，∠BDC=∠BAE，
∵∠BDC+∠ADC=∠BAE+∠ADC=∠BDA=60°，
∴在△ADH中，∠AHD=180°-∠ADC-∠DAB-∠BAE
=180°-∠ADC-（∠DAB+∠BAE）
=180°-60°-60°
=60°；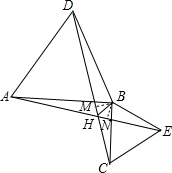
（2）过点B分别作BM⊥CD，NN⊥AE，垂足为点M，N．
∵由（1）知：△ABE≌△DBC，
∴S_△ABE=S_△DBC
∴$\frac{1}{2}×CD×BM=\frac{1}{2}×AE×BN$
∴BM=BN
∴点B在∠DHE的平分线上，
∴BH平分∠AHC．

点评 本题考查了等边三角形性质、三角形的面积、全等三角形的性质和判定、三角形的内角和定理的综合运用，证明△ABE≌△DBC是解决问题的关键．