题目内容
2.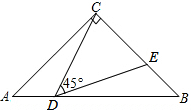 如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=8.点D在边AB上(点D不与点A、B重合),连接CD,作∠CDE=45°,DE与边BC交于点E.
如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=8.点D在边AB上(点D不与点A、B重合),连接CD,作∠CDE=45°,DE与边BC交于点E.(1)求证:△CAD∽△DBE.
(2)当AD=2时,求CE的长.
(3)当△CDE为等腰三角形时,直接写出DB的长.
分析 (1)由在Rt△ABC中,∠ACB=90°,CA=CB,可求得∠A=∠B=45°,又由∠CDE=45°,利用平角与三角形内角和定理,求得∠ADC=∠DEB,继而证得:△CAD∽△DBE;
(2)由AD=2,可求得BD的长,由等腰直角三角形的性质,可求得CA与CB的长,然后由△CAD∽△DBE,根据相似三角形的对应边成比例,即可求得CE的长;
(3)分别从CD=DE与CE=DE去分析求解即可求得答案.
解答 (1)证明:∵∠ACB=90°,CA=CB,
∴∠A=∠B=45°,
又∵∠ADC=180°-45°-∠EDB,∠DEB=180°-45°-∠EDB,
∴∠ADC=∠DEB,
∴△CAD∽△DBE;
(2)解:∵∠ACB=90°,CA=CB,AB=8.
∴CA=CB=$\frac{\sqrt{2}}{2}$AB=4$\sqrt{2}$,DB=AB-AD=8-2=6,
又∵△CAD∽△DBE,
∴$\frac{CA}{DB}=\frac{AD}{BE}$.
即$\frac{{4\sqrt{2}}}{6}=\frac{2}{BE}$,
∴$BE=\frac{{3\sqrt{2}}}{2}$,
∴$CE=CB-BE=4\sqrt{2}-\frac{{3\sqrt{2}}}{2}=\frac{{5\sqrt{2}}}{2}$;
(3)解:∵∠DCE<ACB,
∴CD≠CE,
当CD=DE时,
∵△CAD∽△DBE,
∴$\frac{AC}{BD}$=$\frac{CD}{DE}$=1,
∴DB=AC=4$\sqrt{2}$;
如图, 当DE=CE时,∠ECD=∠EDC=45°,
当DE=CE时,∠ECD=∠EDC=45°,
∵∠ACB=90°,
∴∠ACD=∠ECD=45°,
∵AC=BC,
∴DB=AD=$\frac{1}{2}$AB=4.
∴当△CDE为等腰三角形时,DB=4$\sqrt{2}$或4.
点评 此题属于相似三角形的综合题.考查了相似三角形的判定与性质、等腰直角三角形的性质以及等腰三角形的性质.注意掌握分类讨论思想的应用是解此题的关键.

 阅读快车系列答案
阅读快车系列答案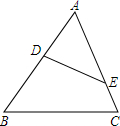 如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )| A. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | B. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
| A. | x+2y=1 | B. | 2x(x-1)-2x+3=0 | C. | $\frac{1}{{x}^{2}}$+4x=3 | D. | x2-2xy=0 |
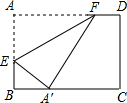 如图,长方形ABCD中,AD=10,AB=8,将长方形ABCD折叠,折痕为EF,点A的对应点A′落在线段BC上,当点A′在BC上移动时,点E、F也随之移动,若限定点E、F分别在线段AB、AD上移动,则点A′在线段BC上可移动的最大距离是4.
如图,长方形ABCD中,AD=10,AB=8,将长方形ABCD折叠,折痕为EF,点A的对应点A′落在线段BC上,当点A′在BC上移动时,点E、F也随之移动,若限定点E、F分别在线段AB、AD上移动,则点A′在线段BC上可移动的最大距离是4.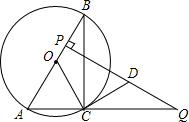 AB是⊙O的直径,AB=2.点C在⊙O上,∠BAC=60°,P是OB上一点,过P作AB的垂线与AC的延长线交于点Q,连结OC,过点C作CD⊥OC交PQ于点D.
AB是⊙O的直径,AB=2.点C在⊙O上,∠BAC=60°,P是OB上一点,过P作AB的垂线与AC的延长线交于点Q,连结OC,过点C作CD⊥OC交PQ于点D.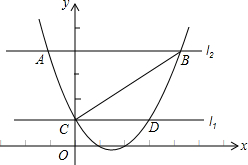 如图,抛物线F:y=ax2+bx+c(a>0)与y轴交于点C,直线l1经过点C且平行于x轴,将直线l1向上平移t个单位得到直线l2,设直线l1与抛物线F的交点为C、D,直线l2与抛物线F的交点为A、B,连接AC、BC.
如图,抛物线F:y=ax2+bx+c(a>0)与y轴交于点C,直线l1经过点C且平行于x轴,将直线l1向上平移t个单位得到直线l2,设直线l1与抛物线F的交点为C、D,直线l2与抛物线F的交点为A、B,连接AC、BC.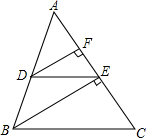 如图,在△ABC中,DE∥BC,BE⊥AC于点E,DF⊥AC于点F,若DE=2,BC=4,BE=2$\sqrt{3}$,且△ABC的周长为12,求△ADE的周长和DF的长度.
如图,在△ABC中,DE∥BC,BE⊥AC于点E,DF⊥AC于点F,若DE=2,BC=4,BE=2$\sqrt{3}$,且△ABC的周长为12,求△ADE的周长和DF的长度.