题目内容
7.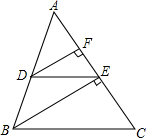 如图,在△ABC中,DE∥BC,BE⊥AC于点E,DF⊥AC于点F,若DE=2,BC=4,BE=2$\sqrt{3}$,且△ABC的周长为12,求△ADE的周长和DF的长度.
如图,在△ABC中,DE∥BC,BE⊥AC于点E,DF⊥AC于点F,若DE=2,BC=4,BE=2$\sqrt{3}$,且△ABC的周长为12,求△ADE的周长和DF的长度.
分析 由平行线得出△ADE∽△ABC,得出相似三角形周长的比等于相似比,即可求出△ADE的周长;证出BE∥DF,得出△ADF∽△ABE,得出相似三角形的对应边成比例,即可求出DF的长.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{△ADE的周长}{△ABC的周长}=\frac{DE}{BC}$=$\frac{2}{4}$=$\frac{1}{2}$=$\frac{AD}{AB}$,
即$\frac{△ADE的周长}{12}=\frac{1}{2}$,
解得:△ADE的周长=6,
∵BE⊥AC,DF⊥AC,
∴BE∥DF,
∴△ADF∽△ABE,
∴$\frac{DF}{BE}=\frac{AD}{AB}$=$\frac{1}{2}$,
即$\frac{DF}{2\sqrt{3}}=\frac{1}{2}$,
解得:DF=$\sqrt{3}$.
点评 本题考查了相似三角形的判定与性质;熟练掌握相似三角形的判定方法,由相似三角形的性质得出比例式是解决问题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
12.下列表格是二次函数y=ax2+bx+c(a≠0)的自变量x与函数y的一些对应值.由此可以判断方程ax2+bx+c=0(a≠0)的一个根在( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.06 |
| A. | 6.17-6.18之间 | B. | 6.18-6.19之间 | C. | 6.19-6.20之间 | D. | 不确定 |
 如图,△ABC中,∠C=90°,AD是∠CAB的角平分线,∠ADC=60°,求∠B的度数.
如图,△ABC中,∠C=90°,AD是∠CAB的角平分线,∠ADC=60°,求∠B的度数.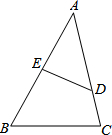 如图,在△ABC中,点D、E分别在边AC、AB上,且$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,若DE=4,则BC=6.
如图,在△ABC中,点D、E分别在边AC、AB上,且$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,若DE=4,则BC=6.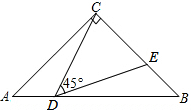 如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=8.点D在边AB上(点D不与点A、B重合),连接CD,作∠CDE=45°,DE与边BC交于点E.
如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=8.点D在边AB上(点D不与点A、B重合),连接CD,作∠CDE=45°,DE与边BC交于点E.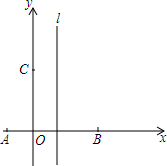 如图,在直角坐标系中,点A、B、C的坐标分别为(-1,0),(3,0),(0,3),过A、B、C三点的抛物线的对称轴为直线l,D为对称轴l上一动点.
如图,在直角坐标系中,点A、B、C的坐标分别为(-1,0),(3,0),(0,3),过A、B、C三点的抛物线的对称轴为直线l,D为对称轴l上一动点.