题目内容
14.将函数y=ax2+c(a>0)的图象向左平移1个单位,平移后的图象过点(-2,y1),(-$\frac{4}{3}$,y2),(1,y3),则y1、y2、y3的大小关系是y2<y1<y3.分析 求出抛物线的对称轴,求出(1,y3)关于对称轴的对称点的坐标,根据抛物线的开口方向和增减性,即可求出答案.
解答 解:将函数y=ax2+c(a>0)的图象向左平移1个单位,
对称轴是直线x=-1,
即二次函数的开口向上,对称轴是直线x=-1,
即在对称轴的左侧y随x的增大而减小,
点(1,y3)关于直线x=-1的对称点是(-3,y3),
∵-3<-2<-$\frac{4}{3}$,
∴y2<y1<y3.
故答案为:y2<y1<y3.
点评 本题考查了二次函数图象与几何变换,二次函数图象上点的坐标特征,主要考查学生的观察能力和分析能力,本题比较典型,但是一道比较容易出错的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.用配方法解方程x2-4x-3=0时,配方后得到的方程为( )
| A. | (x+2)2=0 | B. | (x-2)2=0 | C. | (x+2)2=2 | D. | (x-2)2=7 |
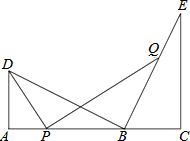 如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.求证:AC=AD+CE.
如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.求证:AC=AD+CE.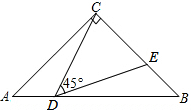 如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=8.点D在边AB上(点D不与点A、B重合),连接CD,作∠CDE=45°,DE与边BC交于点E.
如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=8.点D在边AB上(点D不与点A、B重合),连接CD,作∠CDE=45°,DE与边BC交于点E.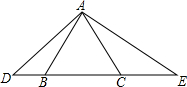 如图,等边三角形ABC中,D为CB延长线上一点,E为BC延长线上点,且满足∠DAE=120°.
如图,等边三角形ABC中,D为CB延长线上一点,E为BC延长线上点,且满足∠DAE=120°.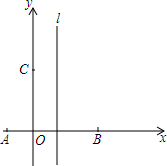 如图,在直角坐标系中,点A、B、C的坐标分别为(-1,0),(3,0),(0,3),过A、B、C三点的抛物线的对称轴为直线l,D为对称轴l上一动点.
如图,在直角坐标系中,点A、B、C的坐标分别为(-1,0),(3,0),(0,3),过A、B、C三点的抛物线的对称轴为直线l,D为对称轴l上一动点.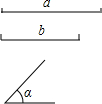 如图,已知线段a、b和∠α,用尺规作一个三角形ABC,使BC=a,AC=b,∠ACB=∠α(要求:不写已知、求作、作法、只画图,保留作图痕迹)
如图,已知线段a、b和∠α,用尺规作一个三角形ABC,使BC=a,AC=b,∠ACB=∠α(要求:不写已知、求作、作法、只画图,保留作图痕迹)