题目内容
16.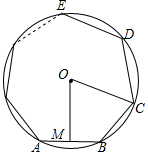 如图,点M是⊙O内接正n边形ABCDE…边AB的中点,连接OM、OC,则∠MOC的度数为( )
如图,点M是⊙O内接正n边形ABCDE…边AB的中点,连接OM、OC,则∠MOC的度数为( )| A. | 180°-$\frac{360°}{n}$ | B. | $\frac{360°}{n}$ | C. | $\frac{540°}{n}$ | D. | $\frac{720°}{n}$ |
分析 连接OB,由正多边形的中心角的定义求出∠BOC和∠MOB,即可得出答案.
解答 解:连接OB,如图所示: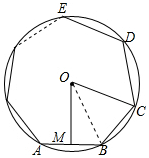
则∠BOC=$\frac{360°}{n}$,
∵点M是⊙O内接正n边形ABCDE…边AB的中点,
∴OM⊥AB,
∴∠MOB=$\frac{1}{2}$×$\frac{360°}{n}$=$\frac{180°}{n}$,
∴∠MOC=$\frac{360°}{n}$+$\frac{180°}{n}$=$\frac{540°}{n}$;
故选:C.
点评 本题考查了正多边形外接圆中心角的性质,圆心角的计算,全等三角形的判定和性质,熟练掌握正多边形外接圆中心角的性质是解题的关键.

练习册系列答案
相关题目
6.$\frac{1}{4}$的算术平方根是( )
| A. | ±$\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{16}$ |
7.若点M(m,n)(mn≠0)在二次函数y=ax2(a≠0)图象上,则下列坐标表示的点也在该抛物线图象上的是( )
| A. | (-m,n) | B. | (n,m) | C. | (m2,n2) | D. | (m,-n) |
4.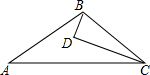 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )| A. | 1 | B. | 1.5 | C. | 2$\sqrt{2}$ | D. | 4 |
1.在△ABC中,如果AB=6,BC=10,那么AC的长可能是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 16 |
8. 如图,AB∥CD,∠E=37°,∠C=20°,则∠EAB=( )
如图,AB∥CD,∠E=37°,∠C=20°,则∠EAB=( )
 如图,AB∥CD,∠E=37°,∠C=20°,则∠EAB=( )
如图,AB∥CD,∠E=37°,∠C=20°,则∠EAB=( )| A. | 37° | B. | 20° | C. | 17° | D. | 57° |
5.对于a>b>c>0,m>n>0(m、n是正整数),成立的关系式是( )
| A. | ambn>bncm>cnam | B. | ambn>cnam>bncm | C. | amcn>ambn>bncm | D. | bnam>cnam>ambn |
6.下列运算正确的是( )
| A. | x3•x4=x12 | B. | (-6x4)÷(-2x2)=3x3 | C. | (-2a2)2=4a4 | D. | (x-3)2=x2-9 |