题目内容
4.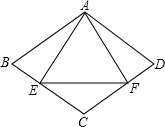 如图,菱形ABCD中,E、F分别为BC、CD上的点,△AEF的三边长和菱形边长相等,求∠BAD的大小.
如图,菱形ABCD中,E、F分别为BC、CD上的点,△AEF的三边长和菱形边长相等,求∠BAD的大小.
分析 由△AEF的边长与菱形ABCD的边长相等得出AB=AE,AF=AD,由菱形的性质、等腰三角形的性质和等边三角形的性质得出方程,求得∠B的度数,即可得出∠BAD的大小.
解答 解:∵△AEF的边长与菱形ABCD的边长相等,
∴△AEF是等边三角形,∠B+∠BAD=180°,AB=AE,AF=AD,
∴∠EAF=60°,∠B=∠AEB,∠D=∠AFD,
设∠B=x,则∠BAD=180°-x,
∠BAE=∠DAF=180°-2x,
即180°-2x+180°-2x+60°=180°-x,
解得:x=80°,
∴∠BAD=180°-80°=100°.
点评 本题考查了菱形的性质、等边三角形的性质、等腰三角形的性质、三角形内角和定理等知识;熟记菱形和等边三角形的性质,根据关于x的等量关系式求x的值是解题的关键.

练习册系列答案
相关题目
16. 如图所示,与∠B构成同位角的共有( )
如图所示,与∠B构成同位角的共有( )
 如图所示,与∠B构成同位角的共有( )
如图所示,与∠B构成同位角的共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
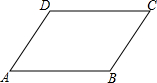 已知:如图,AB∥CD,∠A=∠C,求证:∠B=∠D.
已知:如图,AB∥CD,∠A=∠C,求证:∠B=∠D.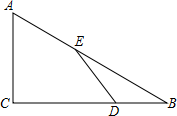 如图,Rt△ABC中,∠C=90°,∠B=30°,BA=6,点E在AB边上,点D是BC边上一点(不与点B、C重合),且AE=ED,线段AE的最小值是( )
如图,Rt△ABC中,∠C=90°,∠B=30°,BA=6,点E在AB边上,点D是BC边上一点(不与点B、C重合),且AE=ED,线段AE的最小值是( )