题目内容
2.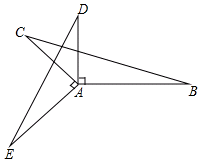 已知:∠EAC=∠DAB=90°,AB=AE,AC=AD,求证:∠E=∠B.
已知:∠EAC=∠DAB=90°,AB=AE,AC=AD,求证:∠E=∠B.
分析 根据全等三角形的性质即可得到结论.
解答 证明:∵∠EAC=∠DAB=90°,
∴∠EAC+∠CAD=∠DAB+∠CAD,
∴∠EAD=∠CAB,
在△EAD与△BAC中,$\left\{\begin{array}{l}{AE=AB}\\{∠EAD=∠CAB}\\{AD=AC}\end{array}\right.$,
∴△EAD≌△CAB(SAS),
∴∠E=∠B.
点评 本题考查了全等三角形的判定和性质;由∠EAC=∠DAB得出∠EAD=∠CAB是正确解决问题的关键,这种方法在三角形全等的证明中经常用到.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,AF⊥BC,垂足为D.
如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,AF⊥BC,垂足为D. 如图,在△ABC中,已知DE∥BC,AD=4,DB=8,BC=9,求DE的长.
如图,在△ABC中,已知DE∥BC,AD=4,DB=8,BC=9,求DE的长.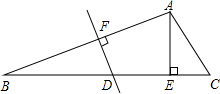 如图,△ABC中,∠C=60°,AB的垂直平分线交BC于点D,DE=6,BD=6$\sqrt{2}$,AE⊥BC于E,求EC的长.
如图,△ABC中,∠C=60°,AB的垂直平分线交BC于点D,DE=6,BD=6$\sqrt{2}$,AE⊥BC于E,求EC的长. 如图,点D在△ABC的AB边上,且DC=DA.
如图,点D在△ABC的AB边上,且DC=DA.