题目内容
13.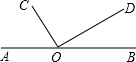 如图,O是直线AB上的一点,OC⊥OD,垂足为O.
如图,O是直线AB上的一点,OC⊥OD,垂足为O.(1)若∠BOD=32°,求∠AOC的度数;
(2)若∠AOC:∠BOD=2:1,直接写出∠BOD的度数.
分析 (1)根据OC⊥OD,∠AOB是平角,∠BOD=32°,即可得到∠AOC的度数;
(2)根据OC⊥OD,∠AOB是平角,∠AOC:∠BOD=2:1,即可得到∠BOD的度数.
解答  解:(1)∵OC⊥OD,
解:(1)∵OC⊥OD,
∴∠COD=90°,
∵∠AOB是平角,
∴∠AOB=180°,
∵∠BOD=32°,
∴∠AOC=180°-∠BOD-∠COD=58°;
(2)∠BOD的度数为30°.理由如下:
∵OC⊥OD,
∴∠COD=90°,
∵∠AOB是平角,
∴∠AOB=180°,
∴∠AOC+∠BOD=90°,
又∵∠AOC:∠BOD=2:1,
∴3∠BOD=90°,
∴∠BOD=30°.
点评 本题主要考查了垂线以及平角的运用,解题时注意:两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
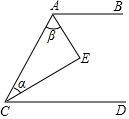 请将下列证明过程补充完整:
请将下列证明过程补充完整: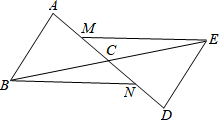 如图,线段AD、BE相交与点C,且△ABC≌△DEC,点M、N分别为线段AC、CD的中点.
如图,线段AD、BE相交与点C,且△ABC≌△DEC,点M、N分别为线段AC、CD的中点.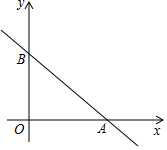 如图,已知直线l:y=-$\frac{3}{4}$x+3分别与x、y轴交于点A和B.
如图,已知直线l:y=-$\frac{3}{4}$x+3分别与x、y轴交于点A和B. 如图AB∥CD,EF分别交AB于点F,交CD于点E,EF与DB交于点G,且EA平分∠CEF,∠BFG=70°.
如图AB∥CD,EF分别交AB于点F,交CD于点E,EF与DB交于点G,且EA平分∠CEF,∠BFG=70°.