题目内容
18．
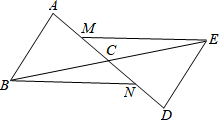如图，线段AD、BE相交与点C，且△ABC≌△DEC，点M、N分别为线段AC、CD的中点．求证：（1）ME=BN；
（2）ME∥BN．
分析 （1）连接BM、EN，根据全等三角形的性质、平行四边形的判定得到四边形MBNE是平行四边形，根据平行四边形的性质证明；
（2）根据平行四边形的性质证明．
解答 证明：（1）
连接BM、EN，
∵△ABC≌△DEC，
∴AC=DC，BC=EC，
∵点M、N分别为线段AC、CD的中点，
∴CM=CN，
∴四边形MBNE是平行四边形，
∴ME=BN；
（2）∵四边形MBNE是平行四边形，
∴ME∥BN．
点评 本题考查的是全等三角形的性质、平行四边形的判定和性质，掌握全等三角形的性质定理、平行四边形的判定定理和性质定理是解题的关键．
练习册系列答案
相关题目
8．
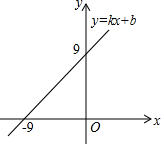一次函数y=kx+b（k，b是常数，k≠0）的图象如图所示，则不等式kx+b＞0的解集是（ ）
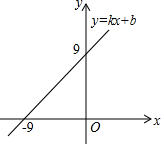一次函数y=kx+b（k，b是常数，k≠0）的图象如图所示，则不等式kx+b＞0的解集是（ ）| A． | x＞-9 | B． | x＞9 | C． | x＜-9 | D． | x＜9 |
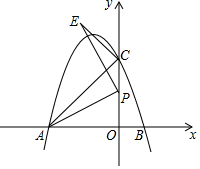如图，抛物线y=-x2-2x+3与x轴交于A、B两点（A在B的左侧），与y轴交于点C，点P是y轴正半轴上一动点，将点A绕点P顺时针旋转90°得到点E，求证：抛物线的顶点D在直线CE上．
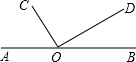如图，O是直线AB上的一点，OC⊥OD，垂足为O．
完成下面的证明．
7．下列说法正确的是（ ）
| A． | -（-8）的立方根是-2 | B． | 立方根等于本身数有-1，0，1 | ||
| C． | $-\sqrt{64}$的立方根为-4 | D． | 一个数的立方根不是正数就是负数 |