题目内容
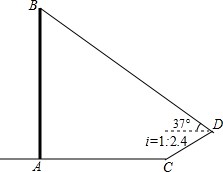 如图,高压电线杆AB垂直地面,测得电线杆AB的底部A到斜坡C的水平距离AC长为15.2米,落在斜坡上的电线杆的影长CD为5.2米,在D点处测得电线杆顶B的仰角为37°.已知斜坡CD的坡比i=1:2.4,求该电线杆AB的高.(参考数据:sin37°=0.6)
如图,高压电线杆AB垂直地面,测得电线杆AB的底部A到斜坡C的水平距离AC长为15.2米,落在斜坡上的电线杆的影长CD为5.2米,在D点处测得电线杆顶B的仰角为37°.已知斜坡CD的坡比i=1:2.4,求该电线杆AB的高.(参考数据:sin37°=0.6)考点:解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题
专题:
分析:过点D作DE垂直AC的延长线于点E,DF垂直AB于点F,根据斜坡CD的坡比i=1:2.4,CD=5.2米,求出CE、DE的长度,然后求出AE和DF的长度,在△BDF中,求出BF的长度,即可求出AB的长度.
解答:解: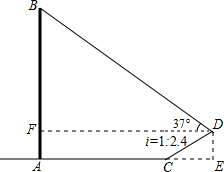 过点D作DE垂直AC的延长线于点E,DF垂直AB于点F,
过点D作DE垂直AC的延长线于点E,DF垂直AB于点F,
则四边形AEDF为矩形,AF=DE,AE=DF,
∵斜坡CD的坡比i=1:2.4,CD=5.2米,
∴设DE=x,CE=2.4x,
CD=
=2.6x=5.2米,
解得:x=2,
则DE=AF=2,CE=4.8,
∴AE=DF=AC+CE=15.2+4.8=20(米),
在△BDF中,
∵∠BDF=37°,DF=20米,
∴BF=DFtan37°=20×0.75=15(米),
∴AB=AF+BF=2+15=17(米).
答:该电线杆AB的高为17米.
 过点D作DE垂直AC的延长线于点E,DF垂直AB于点F,
过点D作DE垂直AC的延长线于点E,DF垂直AB于点F,则四边形AEDF为矩形,AF=DE,AE=DF,
∵斜坡CD的坡比i=1:2.4,CD=5.2米,
∴设DE=x,CE=2.4x,
CD=
| CE2+DE2 |
解得:x=2,
则DE=AF=2,CE=4.8,
∴AE=DF=AC+CE=15.2+4.8=20(米),
在△BDF中,
∵∠BDF=37°,DF=20米,
∴BF=DFtan37°=20×0.75=15(米),
∴AB=AF+BF=2+15=17(米).
答:该电线杆AB的高为17米.
点评:本题考查了解直角三角形的应用,解答本题的关键是根据坡度和仰角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列事件是确定事件的( )
①平分弦的直径垂直于弦
②点P(2,-1)和点Q(-2,1)关于原点对称
③抛一枚硬币,正面朝上
④反比例函数y=-
,若x1<x2,则y1<y2.
①平分弦的直径垂直于弦
②点P(2,-1)和点Q(-2,1)关于原点对称
③抛一枚硬币,正面朝上
④反比例函数y=-
| 2 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
抛物线y=2x2,y=-2x2,y=
x2共有的性质是( )
| 1 |
| 2 |
| A、开口向下 |
| B、对称轴是y轴 |
| C、都有最低点 |
| D、y的值随x的增大而减小 |
下列图形中,既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
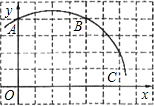 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.若A点的坐标为(0,4),D点的坐标为(7,0).
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.若A点的坐标为(0,4),D点的坐标为(7,0).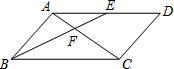 已知:如图,?ABCD中,E是AD中点,BE交AC于点F,设
已知:如图,?ABCD中,E是AD中点,BE交AC于点F,设 如图,在△ABC中,AB=8,∠ABC=30°,∠ACB=45°,则BC的长为
如图,在△ABC中,AB=8,∠ABC=30°,∠ACB=45°,则BC的长为 如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点F,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点F,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.