题目内容
 如图,已知∠1=40°,∠2=140°,∠3=40°,∠4=140°.试说明:a∥b,b∥c,d∥e,a∥c.
如图,已知∠1=40°,∠2=140°,∠3=40°,∠4=140°.试说明:a∥b,b∥c,d∥e,a∥c.考点:平行线的判定
专题:证明题
分析:由条件可分别得到∠1+∠2=180°,可证明a∥b;可求得∠5=∠3,可证明d∥e;由∠3+∠4=180°可求得∠3=∠6,可证明b∥c,由平行的传递性可得a∥c.
解答:证明:
∵∠1=40°,∠2=140°,
∴∠1+∠2=180°,
∴a∥b;
∴∠5=∠1=40°=∠3,
∴d∥e;
∵∠4=140°,且∠6+∠4=180°,
∴∠6=40°=∠3,
∴b∥c;
∴a∥c.
∵∠1=40°,∠2=140°,
∴∠1+∠2=180°,
∴a∥b;
∴∠5=∠1=40°=∠3,
∴d∥e;
∵∠4=140°,且∠6+∠4=180°,
∴∠6=40°=∠3,
∴b∥c;
∴a∥c.
点评:本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
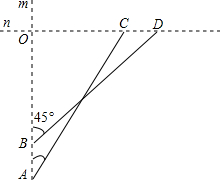 如图,在一次速度测试中,互相垂直的两条轨道m,n上各有一部测试机甲和乙,某时刻甲在A处发现乙在其北偏东30°方向的C处,3min后,甲到达B处,且发现乙在其北偏东45°方向的D处,甲又继续行驶9min到达两条轨道的交叉点O处,已知甲、乙均为匀速行驶,甲的速度是30m/min,试求乙的速度.(
如图,在一次速度测试中,互相垂直的两条轨道m,n上各有一部测试机甲和乙,某时刻甲在A处发现乙在其北偏东30°方向的C处,3min后,甲到达B处,且发现乙在其北偏东45°方向的D处,甲又继续行驶9min到达两条轨道的交叉点O处,已知甲、乙均为匀速行驶,甲的速度是30m/min,试求乙的速度.( 如图,在△ABC上,已知点D是BC的中点,且点D在AB的垂直平分线上.求证:点D也在AC的垂直平分线上.
如图,在△ABC上,已知点D是BC的中点,且点D在AB的垂直平分线上.求证:点D也在AC的垂直平分线上. 如图所示,∠1=∠2=∠3,图中有哪些直线是互相平行的?并说明理由.
如图所示,∠1=∠2=∠3,图中有哪些直线是互相平行的?并说明理由. 如图,直线AB分别交x轴,y轴于点A,B,
如图,直线AB分别交x轴,y轴于点A,B, 如图,GH交AB于N,交CD于P,交EF于M,PQ⊥GH交EF于Q,已知∠1=∠2=54°,∠4=36°,判断AB与EF的位置关系,并说明理由.
如图,GH交AB于N,交CD于P,交EF于M,PQ⊥GH交EF于Q,已知∠1=∠2=54°,∠4=36°,判断AB与EF的位置关系,并说明理由. 如图,平行四边形ABCD中,AC⊥AB,AC与BD相交于O,OC=1,CD=
如图,平行四边形ABCD中,AC⊥AB,AC与BD相交于O,OC=1,CD=

 如图,在边长为1的小正方形组成的网络中,△ABC的三个顶点均在格点上,则cosC=
如图,在边长为1的小正方形组成的网络中,△ABC的三个顶点均在格点上,则cosC=