题目内容
6.如图,在平面直角坐标系中,矩形OABC的边OC在x轴上,OA在y轴上,∠BOC=30°,OC=2$\sqrt{3}$,两动点P、Q分别从O、B两点同时出发,点P以每秒$\sqrt{3}$个单位长度的速度沿线段OC向点C运动,点Q以每秒2个单位长度的速度沿着线段BO向点O运动,当点P运动到点C时,P、Q同时停止,设这两个点运动时间为t(s).(1)求出点A、B的坐标;
(2)当△OPQ的面积为$\frac{3\sqrt{3}}{8}$时,求出t的值及此时点Q的坐标;
(3)在运动过程中,是否存在P、Q两点,使得△PQC沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.
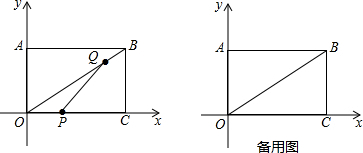
分析 (1)由矩形的性质和已知条件求出OA、AB即可得出A、B的坐标;
(2)作QE⊥OC于E,则QE∥BC,证出△OQE∽△OBC,得出对应边成比例$\frac{QE}{BC}=\frac{OQ}{OB}$,得出QE=2-t,由△OPQ的面积=$\frac{1}{2}$OP•QE,求出t的值,再求出OE,即可得出Q的坐标;
(3)分三种情况:①当PQ=PC时;②当QC=PC时;③PQ=QC时;分别得出t的方程,解方程即可.
解答 解:(1)∵四边形ABCD是矩形,
∴OA=BC,AB=OC=2$\sqrt{3}$,∠OCB=90°,
∵∠BOC=30°,OC=2$\sqrt{3}$,
∴OA=BC=OC•tan30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,
∴OB=2BC=4,
∴A(0,2),B(2$\sqrt{3}$,2);
(2)作QE⊥OC于E,如图1所示: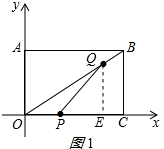 则QE∥BC,
则QE∥BC,
∴△OQE∽△OBC,
∴$\frac{QE}{BC}=\frac{OQ}{OB}$,即$\frac{QE}{2}=\frac{4-2t}{4}$,
∴QE=2-t,
∴△OPQ的面积=$\frac{1}{2}$OP•QE=$\frac{1}{2}$×$\sqrt{3}$t×(2-t)=$\frac{3\sqrt{3}}{8}$,
解得:t=$\frac{1}{2}$或t=$\frac{3}{2}$,
当t=$\frac{1}{2}$时,QE=2-$\frac{1}{2}$=$\frac{3}{2}$,OE=$\sqrt{3}$QE=$\frac{3\sqrt{3}}{2}$;
当t=$\frac{3}{2}$时,QE=2-$\frac{3}{2}$=$\frac{1}{2}$,OE=$\sqrt{3}$QE=$\frac{\sqrt{3}}{2}$;
∴点Q的坐标为($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$),或($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);
(3)存在;分三种情况:如图2所示: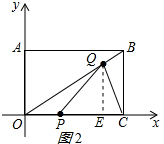
①当PQ=PC时,
∵OP=$\sqrt{3}$t,
∴PC=2$\sqrt{3}$-$\sqrt{3}$t,
由(2)得:OE=$\sqrt{3}$QE=$\sqrt{3}$(2-t),
∴PE=OE-OP=2$\sqrt{3}$-2$\sqrt{3}$t,
∴PQ2=PE2+QE2,
∴(2-t)2+(2$\sqrt{3}$-2$\sqrt{3}$t)2=(2$\sqrt{3}$-$\sqrt{3}$t)2,
解得:t=$\frac{4-\sqrt{6}}{5}$,或t=$\frac{4+\sqrt{6}}{5}$;
②当QC=PC时,QC2=QE2+CE2,
∴(2-t)2+($\sqrt{3}$t)=(2$\sqrt{3}$-$\sqrt{3}$t)2,
解得:t=-4±2$\sqrt{6}$(负值舍去),
∴t=-4+2$\sqrt{6}$;
③PQ=QC时,PE=CE,
∴2$\sqrt{3}$+2$\sqrt{3}$t=$\sqrt{3}$t,
解得:t=$\frac{2}{3}$.
综上所述:t的值为$\frac{4±\sqrt{6}}{5}$,或t=-4+2$\sqrt{6}$,或t=$\frac{2}{3}$.
点评 本题是一次函数综合题目,考查了矩形的性质、相似三角形的判定与性质、三角形面积的计算、三角函数以及坐标与图形特征;本题难度较大,综合性强,特别是(3)中,需要通过分类讨论列出方程,解方程才能得出结果.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案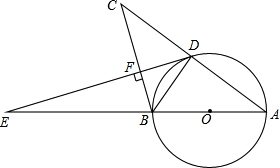 如图,在△ABC中,以AB为直径的⊙O与AC交于D点,过点D作DF⊥BC交AB的延长线于点E,垂足为F,∠FDB=∠A.
如图,在△ABC中,以AB为直径的⊙O与AC交于D点,过点D作DF⊥BC交AB的延长线于点E,垂足为F,∠FDB=∠A.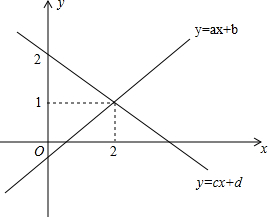 如图,直线y=ax+b与直线y=cx+d相交于点(2,1),则关于x的一元一次方程ax+b=cx+d的解为x=2.
如图,直线y=ax+b与直线y=cx+d相交于点(2,1),则关于x的一元一次方程ax+b=cx+d的解为x=2.