题目内容
15.根据下列条件分别确定函数y=kx+b的解析式:(1)y与x成正比例,当x=5时,y=6;
(2)直线y=kx+b经过点(3,6)与点($\frac{1}{2}$,-$\frac{1}{2}$)
分析 (1)根据y与x成正比例,可设y=kx,把x=5,y=6代入,用待定系数法可求出函数解析式;
(2)将点(3,6)与点($\frac{1}{2}$,-$\frac{1}{2}$)分别代入y=kx+b,组成关于k、b的二元一次方程组,解方程组即可求出k、b的值,从而得到直线的解析式.
解答 解:(1)设y=kx,把x=5,y=6代入,
得5k=6,解得k=$\frac{6}{5}$,
故所求函数解析式为y=$\frac{6}{5}$x;
(2)∵直线y=kx+b经过点(3,6)与点($\frac{1}{2}$,-$\frac{1}{2}$),
∴$\left\{\begin{array}{l}{3k+b=6}\\{\frac{1}{2}k+b=-\frac{1}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{13}{5}}\\{b=-\frac{9}{5}}\end{array}\right.$,
∴所求函数解析式为y=$\frac{13}{5}$x-$\frac{9}{5}$.
点评 本题考查了待定系数法求一次函数与正比例函数的解析式,熟练掌握待定系数法是解题的关键.

练习册系列答案
相关题目
5.64的平方根是( )
| A. | ±8 | B. | ±4 | C. | 8 | D. | 32 |
3.下列式子正确的是( )
| A. | x6÷x3=x2 | B. | (-1)-1=-1 | C. | 4m-2=$\frac{1}{{4{m^2}}}$ | D. | (a2)4=a6 |
10.已知(3x-5y-a)2+|x-1|=0中,y的值小于1,则a的取值范围是( )
| A. | a<-2 | B. | a>-2 | C. | a<8 | D. | 无法确定 |
4.已知圆的面积为7π,估计该圆的半径r所在范围正确的是( )
| A. | 1<r<2 | B. | 2<r<3 | C. | 3<r<4 | D. | 4<r<5 |
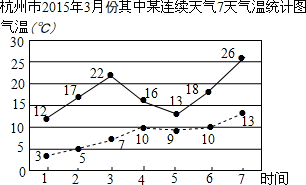 如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):
如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):