题目内容
16.填空和计算:(1)给出下列代数式:$\frac{1}{2}$,$\frac{2x+1}{2x}$,$\frac{x+1}{2}$,x-5,$\frac{2}{{{x^2}-1}}$,$\frac{2-x}{x+2}$,其中有3个是分式;
请你从上述代数式中取出一个分式为$\frac{2x+1}{2x}$,对于所取的分式:①当x≠0时分式有意义;②当x=2时,分式的值为$\frac{5}{4}$.
(2)已知$x=\frac{{\sqrt{3}-\sqrt{2}}}{2}$,$y=\frac{{\sqrt{3}+\sqrt{2}}}{2}$,求代数式x2+6xy+y2的值.
分析 (1).根据分式的意义直接判定即可,进一步利用分式有意义的条件判定和代值计算即可;
(2)先把代数式分组分解,再进一步代入求得数值即可.
解答 解:(1)$\frac{1}{2}$,$\frac{2x+1}{2x}$,$\frac{x+1}{2}$,x-5,$\frac{2}{{{x^2}-1}}$,$\frac{2-x}{x+2}$其中$\frac{2x+1}{2x}$,$\frac{2}{{{x^2}-1}}$,$\frac{2-x}{x+2}$这3个是分式;
取出一个分式为$\frac{2x+1}{2x}$,:①当x≠0时分式有意义;②当x=2时,分式的值为$\frac{5}{4}$.
(2)原式=(x+y)2+4xy=($\frac{\sqrt{3}-\sqrt{2}}{2}$+$\frac{\sqrt{3}+\sqrt{2}}{2}$)2+4×($\frac{\sqrt{3}-\sqrt{2}}{2}$×$\frac{\sqrt{3}+\sqrt{2}}{2}$)=3+4×$\frac{1}{4}$=4.
点评 此题考查二次根式的意义,二次根式有意义的条件,二次根式的化简求值,掌握基本概念、化简的方法是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知圆的面积为7π,估计该圆的半径r所在范围正确的是( )
| A. | 1<r<2 | B. | 2<r<3 | C. | 3<r<4 | D. | 4<r<5 |
11.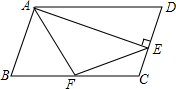 已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )
已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )
 已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )
已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )| A. | ①②④ | B. | ①③ | C. | ②③④ | D. | ①②③④ |
1. 如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,则树的高度为( )
如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,则树的高度为( )
 如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,则树的高度为( )
如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,则树的高度为( )| A. | 6米 | B. | 4.5米 | C. | 4米 | D. | 3米 |
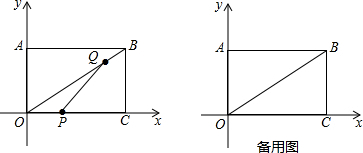
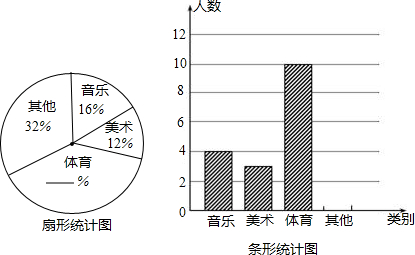
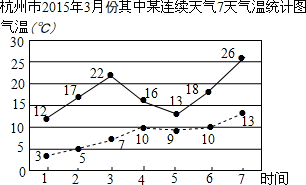 如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):
如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):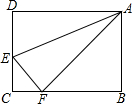 如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.
如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.