题目内容
1.先化简,再求值:($\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{x+2}{{x}^{2}-2x+1}$,其中x=2.分析 按照分式的性质进行化简后代入x=2求值即可.
解答 解:原式=$\frac{3x+4-2(x+1)}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+2}$
=$\frac{x-1}{x+1}$
当x=2时,原式=$\frac{1}{3}$.
点评 本题考查了分式的化简求值的知识,解题的关键是能够对分式进行正确的化简,难度不大.

练习册系列答案
相关题目
11. 如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )
如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )
 如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )
如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )| A. | 56 | B. | 72 | C. | 80 | D. | 104 |
9.下列各式从左到右的变形中,属于因式分解的是( )
| A. | ${x^2}+3x-4=x({x+3-\frac{4}{x}})$ | B. | (x+2)(x-2)=x2-4 | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | $-{x^2}+x-\frac{1}{4}=-{({x-\frac{1}{2}})^2}$ |
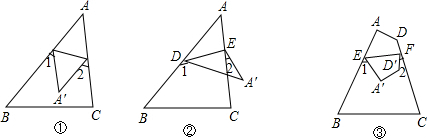
 如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$
如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$ 如图,在平面直角坐标系xoy中,已知点A(2,1)、B(-1,1)、C(-1,-3)、D(2,-3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为(2,-2).
如图,在平面直角坐标系xoy中,已知点A(2,1)、B(-1,1)、C(-1,-3)、D(2,-3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为(2,-2).
 如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是( )
如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是( )



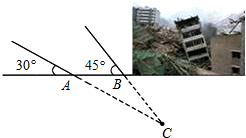 2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20千米.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20千米.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)