题目内容
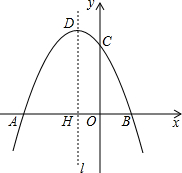 如图,已知抛物线y=ax2+bx+3经过A(-3,0),B(1,0)两点,与y轴交于点C,其顶点为D,对称轴是直线l,l与x轴交于点H.
如图,已知抛物线y=ax2+bx+3经过A(-3,0),B(1,0)两点,与y轴交于点C,其顶点为D,对称轴是直线l,l与x轴交于点H.(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)若E是线段AD上的一个动点(E与A,D不重合),过E点作平行于y轴的直线交抛物线于F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)利用待定系数法求出抛物线的解析式;
(2)因为BC为定值,所以当PB+PC最小时,△PBC的周长最小.
如答图1所示,连接AC交l于点P,由轴对称性质可知,此点P即为所求;
(3)如答图2所示,
①首先根据题意,求出点E、F的坐标,然后利用S=S△AEF+S△DEF=
EF•AH,求出S与m的函数关系式;
②根据关系式,利用二次函数的极值,求出最大值及点E的坐标.
(2)因为BC为定值,所以当PB+PC最小时,△PBC的周长最小.
如答图1所示,连接AC交l于点P,由轴对称性质可知,此点P即为所求;
(3)如答图2所示,
①首先根据题意,求出点E、F的坐标,然后利用S=S△AEF+S△DEF=
| 1 |
| 2 |
②根据关系式,利用二次函数的极值,求出最大值及点E的坐标.
解答:解:(1)由题意可知:
,解得:
,
∴抛物线的解析式为:y=-x2-2x+3.
(2)∵y=-x2-2x+3,∴C(0,3).
∵△PBC的周长为:PB+PC+BC,BC是定值,
∴当PB+PC最小时,△PBC的周长最小.
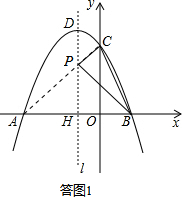
如答图1所示,点A、B关于对称轴l对称,连接AC交l于点P,则点P为所求的点.
∵AP=BP,
∴△PBC周长的最小值是:PB+PC+BC=AC+BC.
∵A(-3,0),B(1,0),C(0,3),
∴AC=3
,BC=
.
∴△PBC周长的最小值是:3
+
.
(3)如答图2,
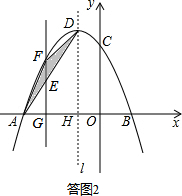
①∵抛物线y=-x2-2x+3的顶点D坐标为(-1,4),A(-3,0),
∴直线AD的解析式为:y=2x+6.
∵点E的横坐标为m,
∴E(m,2m+6),F(m,-m2-2m+3)
∴EF=-m2-2m+3-(2m+6)=-m2-4m-3.
∴S=S△AEF+S△DEF
=
EF•AG+
EF•GH=
EF•AH
=
×(-m2-4m-3)×2
=-m2-4m-3;
②S=-m2-4m-3=-(m+2)2+1
∴当m=-2时,S最大,最大值为1.此时点E的坐标为(-2,2).
|
|
∴抛物线的解析式为:y=-x2-2x+3.
(2)∵y=-x2-2x+3,∴C(0,3).
∵△PBC的周长为:PB+PC+BC,BC是定值,
∴当PB+PC最小时,△PBC的周长最小.

如答图1所示,点A、B关于对称轴l对称,连接AC交l于点P,则点P为所求的点.
∵AP=BP,
∴△PBC周长的最小值是:PB+PC+BC=AC+BC.
∵A(-3,0),B(1,0),C(0,3),
∴AC=3
| 2 |
| 10 |
∴△PBC周长的最小值是:3
| 2 |
| 10 |
(3)如答图2,

①∵抛物线y=-x2-2x+3的顶点D坐标为(-1,4),A(-3,0),
∴直线AD的解析式为:y=2x+6.
∵点E的横坐标为m,
∴E(m,2m+6),F(m,-m2-2m+3)
∴EF=-m2-2m+3-(2m+6)=-m2-4m-3.
∴S=S△AEF+S△DEF
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=-m2-4m-3;
②S=-m2-4m-3=-(m+2)2+1
∴当m=-2时,S最大,最大值为1.此时点E的坐标为(-2,2).
点评:本题是二次函数压轴题,综合考查了二次函数的图象与性质、待定系数法、图形面积计算、轴对称-最短路线等知识点,题目较为典型.

练习册系列答案
相关题目
下列命题正确的是( )
| A、圆是轴对称图形,直径是它的对称轴 |
| B、在同圆或等圆中,相等的弦所对的圆周角相等 |
| C、垂直于弦的直径平分弦 |
| D、垂直于半径的直线是这个圆的切线 |
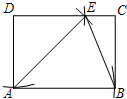 如图,在矩形ABCD中,以点D为圆心,DA长为半径画弧,交CD于点E,以点A为圆心,AE长为半径画弧,恰好经过点B,连结BE、AE.求∠EBC的度数.
如图,在矩形ABCD中,以点D为圆心,DA长为半径画弧,交CD于点E,以点A为圆心,AE长为半径画弧,恰好经过点B,连结BE、AE.求∠EBC的度数.
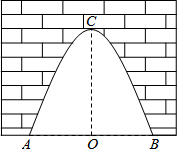 如图:某古城有一个抛物线形石拱门,拱门地面的最大宽度AB=4米,拱门的最大高度OC=4米.
如图:某古城有一个抛物线形石拱门,拱门地面的最大宽度AB=4米,拱门的最大高度OC=4米.