题目内容
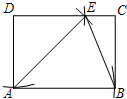 如图,在矩形ABCD中,以点D为圆心,DA长为半径画弧,交CD于点E,以点A为圆心,AE长为半径画弧,恰好经过点B,连结BE、AE.求∠EBC的度数.
如图,在矩形ABCD中,以点D为圆心,DA长为半径画弧,交CD于点E,以点A为圆心,AE长为半径画弧,恰好经过点B,连结BE、AE.求∠EBC的度数.考点:矩形的性质,等腰直角三角形
专题:
分析:根据题意可得AD=DE,AE=AB,再根据矩形的性质可得∠D=∠ABC=∠DAB=90°,然后根据等腰三角形的性质分别算出∠DAE和∠EAB,再根据叫的和差关系可得答案.
解答:解:由题意得:AD=DE,AE=AB,
∵四边形ABCD是矩形,
∴∠D=∠ABC=∠DAB=90°,
∵AD=DE,
∴∠DAE=45°,
∴∠EAB=45°,
∵AE=AB,
∴∠EBA=∠AEB=
=67.5°,
∴∠EBC=90°-67.5°=22.5°.
∵四边形ABCD是矩形,
∴∠D=∠ABC=∠DAB=90°,
∵AD=DE,
∴∠DAE=45°,
∴∠EAB=45°,
∵AE=AB,
∴∠EBA=∠AEB=
| 180°-45° |
| 2 |
∴∠EBC=90°-67.5°=22.5°.
点评:此题主要考查了矩形的性质,以及等腰三角形的性质,关键是掌握矩形的四个角都是直角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
甲地的海拔高度6米,乙地比甲地低8米,乙地的海拔高度为( )
| A、-14米 | B、-2米 |
| C、2米 | D、14米 |
下列运算不正确的是( )
| A、a5+a5=2a5 |
| B、(-2a2)2=-4a4 |
| C、2a2•a-1=2a |
| D、(2a3-a2)÷a2=2a-1 |
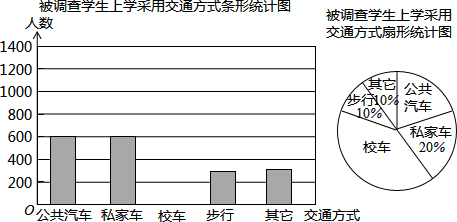
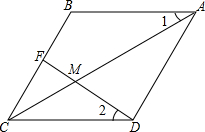 如图,在菱形ABCD中,点M是对角线AC上一点,且MC=MD.连接DM并延长,交边BC于点F.
如图,在菱形ABCD中,点M是对角线AC上一点,且MC=MD.连接DM并延长,交边BC于点F.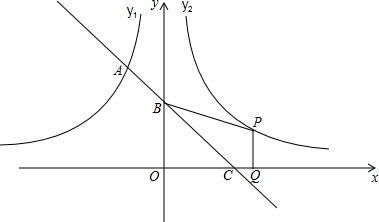
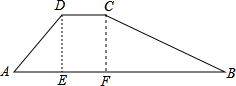 如图,水库大坝截面的迎水坡AD坡比(DE与AE的长度之比)为4:3背水坡BC坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,求大坝的截面面积和周长.
如图,水库大坝截面的迎水坡AD坡比(DE与AE的长度之比)为4:3背水坡BC坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,求大坝的截面面积和周长.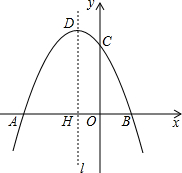 如图,已知抛物线y=ax2+bx+3经过A(-3,0),B(1,0)两点,与y轴交于点C,其顶点为D,对称轴是直线l,l与x轴交于点H.
如图,已知抛物线y=ax2+bx+3经过A(-3,0),B(1,0)两点,与y轴交于点C,其顶点为D,对称轴是直线l,l与x轴交于点H.