题目内容
一辆客车、一辆货车和一辆小轿车在一条笔直的公路上朝同一方向匀速行驶．在某一时刻，客车在前，小轿车在后，货车在客车与小轿车的正中间．过了10分钟，小轿车追上了货车；又过了20分钟，货车追上了客车．问小轿车追上客车，需要多长时间？
考点：一元一次方程的应用
专题：
分析：由于在某一时刻，货车在前，小轿车在后，客车在货车与小轿车的中间，所以设在某一时刻，货车与客车、小轿车的距离均为S千米，小轿车、货车、客车的速度分别为a、b、c（千米/分），由过了10分钟，小轿车追上了客车可以列出方程10（a-b）=S，由又过了5分钟，小轿车追上了货车列出方程15（a-c）=2S，由再过t分钟，客车追上了货车列出方程（t+10+5）（b-c）=S，联立所有方程求解即可求出t的值．
解答：解：设在某一时刻，货车与客车、小轿车的距离均为S千米，小轿车、货车、客车的速度分别为a、b、c（千米/分），
由题意可得：
10（a-b）=S ①
15（a-c）=2S ②
（t+10+5）（b-c）=S ③
由②×2-①×3 得
30（b-c）=S，④
④代入③中得
∴t+10+5=30，
∴t=30-10-5=15（分钟）．
答：小轿车追上客车，需要15分钟．
由题意可得：
10（a-b）=S ①
15（a-c）=2S ②
（t+10+5）（b-c）=S ③
由②×2-①×3 得
30（b-c）=S，④
④代入③中得
∴t+10+5=30，
∴t=30-10-5=15（分钟）．
答：小轿车追上客车，需要15分钟．
点评：此题主要考查了方程的应用-追及问题．行程问题中的追及问题，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．
练习册系列答案
相关题目
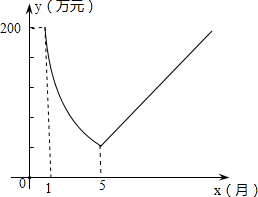保护生态环境，建设绿色社会已经从理念变为人们的行动．某化工厂2014年1月的利润为200万元．设2014年1月为第1个月，第x个月的利润为y万元．由于排污超标，该厂决定从2014年1月底起适当限产，并投入资金进行治污改造，导致月利润明显下降，从1月到5月，y与x成反比例．到5月底，治污改造工程顺利完工，从这时起，该厂每月的利润比前一个月增加20万元（如图）．如果
=
成立，则x的范围（ ）
| ||
|
|
| A、x≥0 | B、x≥1 |
| C、0＜x≤1 | D、x＞0 |
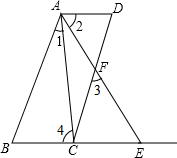如图，已知AD∥BE，AB∥CD，∠1=∠2．求证：∠3=∠4．