题目内容
8. 如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )
如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )| A. | 2 | B. | 3 | C. | 4 | D. | 4.5 |
分析 由BC∥AD,推出△AED∽△CEB,得$\frac{AD}{BC}$=$\frac{AE}{EC}$,由此即可解决问题.
解答 解:∵BC∥AD,
∴△AED∽△CEB,
∴$\frac{AD}{BC}$=$\frac{AE}{EC}$,
∴$\frac{3}{BC}$=$\frac{2}{3}$,
∴BC=4.5,
故选D.
点评 本题考查相似三角形的判定和性质、平行线的性质等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.

练习册系列答案
相关题目
18.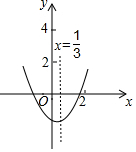 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②abc>0,③a-b+c>0,④2a-3b=0,⑤c-4b>0.其中正确结论的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②abc>0,③a-b+c>0,④2a-3b=0,⑤c-4b>0.其中正确结论的个数有( )
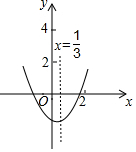 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②abc>0,③a-b+c>0,④2a-3b=0,⑤c-4b>0.其中正确结论的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②abc>0,③a-b+c>0,④2a-3b=0,⑤c-4b>0.其中正确结论的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.在函数y=$\frac{\sqrt{2-x}}{x}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x≤2且x≠0 | C. | x<2 | D. | x>2且x≠0 |
13.二次函数y=(x-1)2-3的最小值是( )
| A. | 2 | B. | 1 | C. | -2 | D. | -3 |
20.已知二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
(1)求二次函数的表达式,并写出这个二次函数图象的顶点坐标;
(2)求出该函数图象与x轴的交点坐标.
| x | … | -2 | -1 | 0 | 2 | … |
| y | … | -3 | -4 | -3 | 5 | … |
(2)求出该函数图象与x轴的交点坐标.
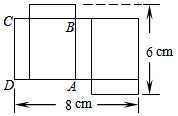 如图,一个长方体的表面展开图中四边形ABCD是正方形,则根据图中数据可得原长方体的体积是12cm3.
如图,一个长方体的表面展开图中四边形ABCD是正方形,则根据图中数据可得原长方体的体积是12cm3. 如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=70°,则∠BCE的度数为70°.
如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=70°,则∠BCE的度数为70°. 有理数a,b,c在数轴上的位置如图所示,化简|a+c|-|a-b|+|b+c|-|b|.
有理数a,b,c在数轴上的位置如图所示,化简|a+c|-|a-b|+|b+c|-|b|.