题目内容
20.已知二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:| x | … | -2 | -1 | 0 | 2 | … |
| y | … | -3 | -4 | -3 | 5 | … |
(2)求出该函数图象与x轴的交点坐标.
分析 (1)由待定系数法即可得出答案;
(2)求出y=0时x的值,即可得出答案.
解答 解:(1)由题意,得c=-3.
将点(2,5),(-1,-4)代入,得$\left\{\begin{array}{l}4a+2b-3=5\\ a-b-3=-4.\end{array}\right.$
解得$\left\{\begin{array}{l}a=1\\ b=2.\end{array}\right.$
∴y=x2+2x-3.
顶点坐标为(-1,-4).
(2)当y=0时,x2+2x-3,
解得:x=-3或x=1,
∴函数图象与x轴的交点坐标为(-3,0),(1,0).
点评 本题考查了待定系数法求二次函数的解析式、抛物线与x轴的交点;求出二次函数的解析式是解决问题的关键.

练习册系列答案
相关题目
8. 如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )
如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )
 如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )
如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )| A. | 2 | B. | 3 | C. | 4 | D. | 4.5 |
15.已知圆锥的底面半径为2cm,母线长为3cm,则它的侧面展开图的面积为( )
| A. | 18πcm2 | B. | 12πcm2 | C. | 6πcm2 | D. | 3πcm2 |
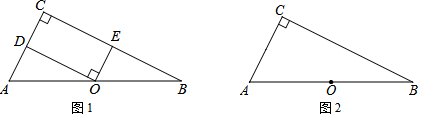
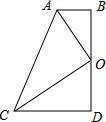 如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC. 已知:△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
已知:△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.