题目内容
18.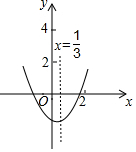 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②abc>0,③a-b+c>0,④2a-3b=0,⑤c-4b>0.其中正确结论的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②abc>0,③a-b+c>0,④2a-3b=0,⑤c-4b>0.其中正确结论的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由抛物线的开口方向判断a的符号,由抛物线与y轴的交点得出c的值,然后根据图象经过的点的情况进行推理,进而对所得结论进行判断.
解答 解:抛物线的开口向上,则a>0;
对称轴为x=-$\frac{b}{2a}$=$\frac{1}{3}$,即3b=-2a,故b<0;
抛物线交y轴于负半轴,则c<0;
①由以上c<0,正确;
②由a>0,b<0,c<0,得abc>0,正确;
③由图知:当x=-1时,y>0,则a-b+c>0,正确;
④由对称轴知:3b=-2a,即3b+2a=0,错误;
⑤由对称轴知:3b=-2a,即a=-$\frac{3}{2}$b,函数解析式可写作y=-$\frac{3}{2}$bx2+bx+c;
由图知:当x=2时,y>0,即-$\frac{3}{2}$b×4+2b+c>0,即c-4b>0,故⑤正确;
∴正确的结论有四个:①②③⑤.
故选:D.
点评 本题考查了二次项系数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
9.下列等式从左到右的变形,属于因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x2-9=(x+3)(x-3) | C. | (x+1)(x+2)=x2+3x+2 | D. | x2+2x+1=x(x+2)+1 |
6. 如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )
如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )
 如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )
如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
3.已知-x2m-3+1=7是关于x的一元一次方程,则m的值是( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
8. 如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )
如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )
 如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )
如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )| A. | 2 | B. | 3 | C. | 4 | D. | 4.5 |
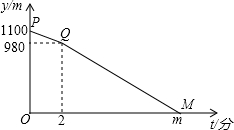 已知A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象解答:
已知A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象解答: