题目内容
 如图,已知△ABC,作一条与BC平行的直线,把△ABC划分成两部分.要使划分成的三角形与四边形的面积之比为1:2,可怎样做?如果要使划分成的两部分的面积之比为1:n呢?
如图,已知△ABC,作一条与BC平行的直线,把△ABC划分成两部分.要使划分成的三角形与四边形的面积之比为1:2,可怎样做?如果要使划分成的两部分的面积之比为1:n呢?考点:作图—应用与设计作图
专题:
分析:首先作出以1为一条直角边,斜边是2的直角三角形,则另一条直角边长是
,作射线,截取AF=1,AG=
,连接BG,作FD∥BG,然后作DE∥BC即可.
| 3 |
| 3 |
解答:解:

DE就是所求的线段.
如果要使划分成的两部分的面积之比为1:n,同样可以得到两个三角形的面积的比是
,则边长的比是
,如上作出AF=1,AG=
,然后连接BG,作FD∥BG,然后作DE∥BC即可.

DE就是所求的线段.
如果要使划分成的两部分的面积之比为1:n,同样可以得到两个三角形的面积的比是
| 1 |
| n+1 |
| 1 | ||
|
| 1+n |
点评:本题考查了勾股定理和平行线分线段成比例定理,正确理解定理的内容是关键.

练习册系列答案
相关题目
我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,若一个四边形ABCD的中点四边形是一个菱形,则四边形ABCD一定满足( )
| A、是菱形 |
| B、对角线相等 |
| C、对角线垂直 |
| D、对角线互相平分 |
若
值为0,则x的值为( )
| x2-9 |
| x2-x-6 |
| A、±3 | B、-3 | C、3 | D、不存在 |
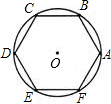 如图,在一张圆形纸片上剪下一个面积最大的正六边形纸片ABCDEF,它的边长是24cm,
如图,在一张圆形纸片上剪下一个面积最大的正六边形纸片ABCDEF,它的边长是24cm, |
| AB |
| A、6πcm | B、8πcm |
| C、36πcm | D、96πcm |
 如图,AB=2AC,BD=2AF,又BD∥AC,点B,A,E在同一条直线上.求证:△ABD∽△CAE.
如图,AB=2AC,BD=2AF,又BD∥AC,点B,A,E在同一条直线上.求证:△ABD∽△CAE.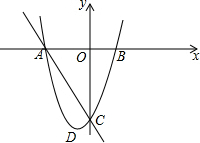 如图,抛物线y=
如图,抛物线y= 如图所示,AB∥CD,你能探究α、β、γ之间的关系吗?试试看.
如图所示,AB∥CD,你能探究α、β、γ之间的关系吗?试试看. 如图,OA⊥OD,OC⊥OB.
如图,OA⊥OD,OC⊥OB.