题目内容
【试题背景】
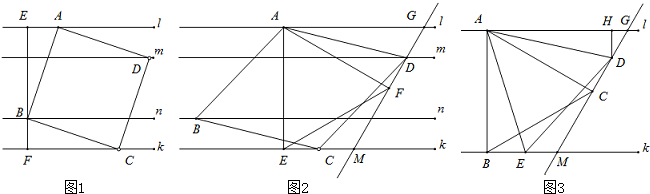
已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”.
【探究1】
(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F,求正方形ABCD的边长.
【探究2】
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,则矩形ABCD的宽为 .(直接写出结果即可)
【探究3】
如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l、k于点G、点M.求证:EC=DF.
【拓展】
(4)如图3,l∥k,等边△ABC的顶点A、B分别落在直线l、k上,AB⊥k于点B,且AB=4,∠ACD=90°,直线CD分别交直线l、k于点G、点M,点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.
猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.
已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”.

【探究1】
(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F,求正方形ABCD的边长.
【探究2】
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,则矩形ABCD的宽为
【探究3】
如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l、k于点G、点M.求证:EC=DF.
【拓展】
(4)如图3,l∥k,等边△ABC的顶点A、B分别落在直线l、k上,AB⊥k于点B,且AB=4,∠ACD=90°,直线CD分别交直线l、k于点G、点M,点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.
猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.
考点:四边形综合题
专题:
分析:(1)证明△ABE≌△BCF,即可求得AE的长,然后利用勾股定理即可求解;
(2)过B作BE⊥l于点E,交k于点F,易证△AEB∽△BCF,然后分AB是长和AB是宽两种情况进行讨论求得;
(3)连接AC,证明直角△AEC≌直角△AFD即可证得;
(4)首先证明AM⊥BC,然后证明Rt△ABE≌Rt△ACD,得到∠BAE=∠CAD,则AM⊥ED,即可证得BC∥DE.
(2)过B作BE⊥l于点E,交k于点F,易证△AEB∽△BCF,然后分AB是长和AB是宽两种情况进行讨论求得;
(3)连接AC,证明直角△AEC≌直角△AFD即可证得;
(4)首先证明AM⊥BC,然后证明Rt△ABE≌Rt△ACD,得到∠BAE=∠CAD,则AM⊥ED,即可证得BC∥DE.
解答:解:(1)∵l∥k,BE⊥l,
∴∠BFC=∠BEA=90°,
∴∠ABE+∠BAE=90°,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC.
∴∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF,
∴AE=BF,
∵d1=d3=1,d2=2,
∴BE=3,AE=1,
在直角△ABE中,AB=
=
=
,
即正方形的边长是
;
(2)过B作BE⊥l于点E,反向延长BE交k于点F.
则BE=1,BF=3,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABE+∠FBC=90°,
又∵直角△ABE中,∠ABE+∠EAB=90°,
∴∠FBC=∠EAB,
∴△AEB∽△BFC,
当AB是较短的边时,如图(a),
AB=
BC,则AE=
BF=
,
在直角△ABE中,AB=
=
;
当AB是长边时,如图(b),
同理可得:BC=
;
故答案为:
或
;
(3)证明:如解答图②,连接AC,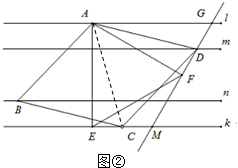
∵四边形ABCD是菱形,且∠ADC=60°,
∴AC=AD,
∵△AEF是等边三角形,
∴AE=AF,
∵AE⊥k,∠AFD=90°,
∴∠AEC=∠AFD=90°,
∴直角△AEC≌直角△AFD,
∴EC=DF;
(4)当2<DH<4时(C点离l的距离为2,D点必在C点下方),BC∥DE.理由如下:
如图③,当2<DH<4时,点D在线段CM上,连接AM.
∵∠ABM=∠ACM=90°,AB=AC,AM=AM,
∴Rt△ABM≌Rt△ACM,
∴∠BAM=∠CAM,
∴AM⊥BC,
又∵AD=AE,AB=AC,
∴Rt△ABE≌Rt△ACD,
∴∠BAE=∠CAD,
∴∠EAM=∠DAM,
∴AM⊥ED.
∴BC∥DE.
∴∠BFC=∠BEA=90°,
∴∠ABE+∠BAE=90°,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC.
∴∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF,
∴AE=BF,
∵d1=d3=1,d2=2,
∴BE=3,AE=1,
在直角△ABE中,AB=
| BE2+AE2 |
| 32+12 |
| 10 |
即正方形的边长是
| 10 |
(2)过B作BE⊥l于点E,反向延长BE交k于点F.
则BE=1,BF=3,
∵四边形ABCD是矩形,

∴∠ABC=90°,
∴∠ABE+∠FBC=90°,
又∵直角△ABE中,∠ABE+∠EAB=90°,
∴∠FBC=∠EAB,
∴△AEB∽△BFC,
当AB是较短的边时,如图(a),
AB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
在直角△ABE中,AB=
12+(
|
| ||
| 2 |
当AB是长边时,如图(b),
同理可得:BC=
| ||
| 2 |
故答案为:
| ||
| 2 |
| ||
| 2 |
(3)证明:如解答图②,连接AC,

∵四边形ABCD是菱形,且∠ADC=60°,
∴AC=AD,
∵△AEF是等边三角形,
∴AE=AF,
∵AE⊥k,∠AFD=90°,
∴∠AEC=∠AFD=90°,
∴直角△AEC≌直角△AFD,
∴EC=DF;
(4)当2<DH<4时(C点离l的距离为2,D点必在C点下方),BC∥DE.理由如下:
如图③,当2<DH<4时,点D在线段CM上,连接AM.
∵∠ABM=∠ACM=90°,AB=AC,AM=AM,
∴Rt△ABM≌Rt△ACM,

∴∠BAM=∠CAM,
∴AM⊥BC,
又∵AD=AE,AB=AC,
∴Rt△ABE≌Rt△ACD,
∴∠BAE=∠CAD,
∴∠EAM=∠DAM,
∴AM⊥ED.
∴BC∥DE.
点评:本题考查了全等三角形的判定与性质以及相似三角形的判定与性质,正确构造相似的三角形是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
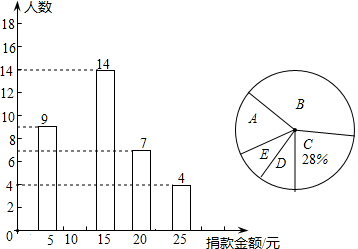 某学校九年级一班的全体同学长期帮助一名孤寡老人,2014年3月份为了达成老人的一个心愿,该班组织了一次捐款活动,捐款情况的部分统计如图.
某学校九年级一班的全体同学长期帮助一名孤寡老人,2014年3月份为了达成老人的一个心愿,该班组织了一次捐款活动,捐款情况的部分统计如图.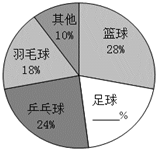 某校课外活动小组为了了解学生最喜欢的球类运动的情况,随机抽查了该校学生,调查数据整理如图,请根据扇形统计图解答以下问题:
某校课外活动小组为了了解学生最喜欢的球类运动的情况,随机抽查了该校学生,调查数据整理如图,请根据扇形统计图解答以下问题: