题目内容
7.k取什么值时,关于x的方程4x2-(k+2)x+k-1=0有两个相等的实数根?求出这时方程的根.分析 由方程有两个相等的实数根结合根的判别式,即可得出关于k的一元二次方程,解之即可得出k值,将k值代入原方程中,解之即可得出方程的根.
解答 解:∵关于x的方程4x2-(k+2)x+k-1=0有两个相等的实数根,
∴△=[-(k+2)]2-4×4(k-1)=k2-12k+20=(k-2)(k-10)=0,
解得:k1=2,k2=10.
当k=2时,原方程为4x2-4x+1=0,
解得:x1=x2=$\frac{1}{2}$;
当k=10时,原方程为4x2-12x+9=0,
解得:x1=x2=$\frac{3}{2}$.
点评 本题考查了根的判别式以及因式分解法解一元二次方程,牢记“当△=0时,方程有两个相等的实数根”是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
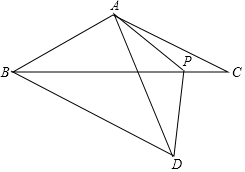 如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4.
如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4. 如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.
如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.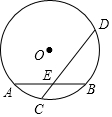 如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )
如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )